
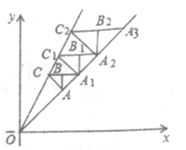
【題目】如圖,在平面直角坐標系第一象限內,直線![]() 與直線
與直線![]() 的內部作等腰
的內部作等腰![]() ,使
,使![]() ,邊
,邊![]() 軸,
軸,![]() 軸,
軸,![]() 在直線
在直線![]() 上,點C在直線
上,點C在直線![]() 上,CB的延長線交直線
上,CB的延長線交直線![]() 于點
于點![]() ,作等腰
,作等腰![]() ,使
,使![]() 軸,
軸,![]() 軸,點
軸,點![]() 在直線
在直線![]() 上,按此規律,則等腰
上,按此規律,則等腰![]() 的腰長為_______.
的腰長為_______.
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,拋物線y=ax2﹣2ax+4(a<0)交x軸于點A、B,與y軸交于點C,AB=6.
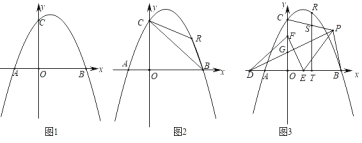
(1)如圖1,求拋物線的解析式;
(2)如圖2,點R為第一象限的拋物線上一點,分別連接RB、RC,設△RBC的面積為s,點R的橫坐標為t,求s與t的函數關系式;
(3)在(2)的條件下,如圖3,點D在x軸的負半軸上,點F在y軸的正半軸上,點E為OB上一點,點P為第一象限內一點,連接PD、EF,PD交OC于點G,DG=EF,PD⊥EF,連接PE,∠PEF=2∠PDE,連接PB、PC,過點R作RT⊥OB于點T,交PC于點S,若點P在BT的垂直平分線上,OB﹣TS=![]() ,求點R的坐標.
,求點R的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個芭蕾舞團演員的身高(單位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
兩組芭蕾舞團演員身高的方差較小的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.擲一枚質地均勻的正方體骰子,骰子停止轉動后,5點朝上是必然事件
B.審查書稿中有哪些學科性錯誤適合用抽樣調查法
C.甲乙兩人在相同條件下各射擊10次,他們的成績的平均數相同,方差分別是![]() =0.4,
=0.4,![]() =0.6,則甲的射擊成績較穩定
=0.6,則甲的射擊成績較穩定
D.擲兩枚質地均勻的硬幣,“兩枚硬幣都是正面朝上”這一事件發生的概率為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
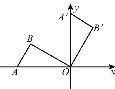
【題目】如圖,將置于平面直角坐標系中的三角板AOB繞O點順時針旋轉90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,則B'點的坐標為 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
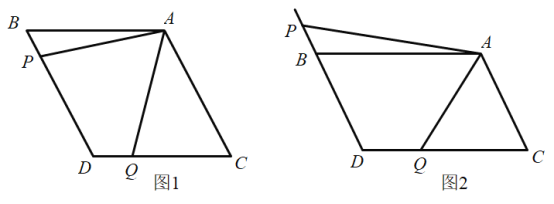
【題目】如圖1,![]() 中,
中,![]() ,
,![]() 分別是
分別是![]() 上的點,且滿足
上的點,且滿足![]() .
.
(1)求證:![]()
(2)在圖1中,是否存在與AP相等的線段?若存在,請找出來,并加以證明;若不存在,說明理由.
(3)若將“![]() 為
為![]() 上的點”改為:“
上的點”改為:“![]() 為DB延長線上的點”其他條件不變(如圖2)若
為DB延長線上的點”其他條件不變(如圖2)若![]() ,求線段
,求線段![]() 之間的數量關系(用含
之間的數量關系(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,將直角的頂點E放在正方形ABCD的對角線AC上,使角的一邊交CD于點F,另一邊交CB或其延長線于點G,求![]() 的值;
的值;
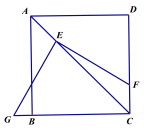
(2)如圖,將(1)中的“正方形ABCD”改成“矩形ABCD”,其他條件不變.若AB=m,BC=n,試求![]() 的值;
的值;
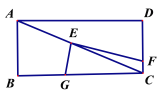
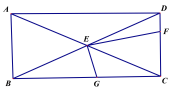
(3)如圖,將直角頂點E放在矩形ABCD的對角線交點,EF、EG分別交CD與CB于點F、G,且EC平分∠FEG.若AB=2,BC=4,直接寫出EG、EF 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當白色小正方形個數按![]() 等于1,2,3,…時的某種規律增加時,由白色小正方形和黑色小正方形組成的圖形分別如圖所示,則第
等于1,2,3,…時的某種規律增加時,由白色小正方形和黑色小正方形組成的圖形分別如圖所示,則第![]() 個圖形中白色小正方形和黑色小正方形的個數總和等于______.(用
個圖形中白色小正方形和黑色小正方形的個數總和等于______.(用![]() 表示,
表示,![]() 是正整數)
是正整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某制藥廠需要緊急生產一批能有效緩解“新冠肺炎”的藥品,要求必須在12天(含12天)內完成.為了加快生產,車間采取工人加班,機器不停的生產方式,這樣每天藥品的產量![]() (噸)是時間
(噸)是時間![]() (天)的一次函數,且滿足如下表中所對應的數量關系.由于機器負荷運轉產生損耗,平均生產每噸藥品的成本
(天)的一次函數,且滿足如下表中所對應的數量關系.由于機器負荷運轉產生損耗,平均生產每噸藥品的成本![]() (元)與時間
(元)與時間![]() (天)的關系滿足如圖所示的函數圖象.
(天)的關系滿足如圖所示的函數圖象.
時間 | 2 | 4 |
每天產量 | 24 | 28 |
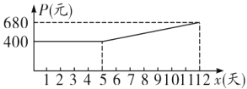
(1)求藥品每天的產量![]() (噸)與時間
(噸)與時間![]() (天)之間的函數關系式;
(天)之間的函數關系式;
(2)當![]() 時,直接寫出
時,直接寫出![]() (元)與時間
(元)與時間![]() (天)的函數關系是
(天)的函數關系是![]() ;
;
(3)若這批藥品的價格為1400元/噸,每天的利潤設為![]() 元,求哪一天的利潤最高,最高利潤是多少?(利潤
元,求哪一天的利潤最高,最高利潤是多少?(利潤![]() 售價
售價![]() 成本)
成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com