
【題目】已知,AB是⊙O的直徑,AB=8,點C在⊙O的半徑OA上運動,PC⊥AB,垂足為C,PC=5,PT為⊙O的切線,切點為T.
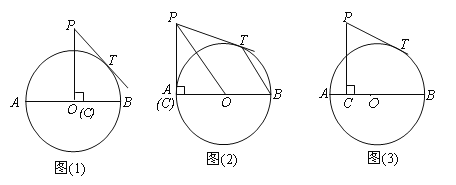
⑴如圖⑴,當C點運動到O點時,求PT的長;
⑵如圖⑵,當C點運動到A點時,連結PO、BT,求證:PO∥BT;
⑶如圖⑶,設![]() ,
,![]() ,求
,求![]() 與
與![]() 的函數關系式及
的函數關系式及![]() 的最小值.
的最小值.
【答案】(1)3;(2)證明見解析;(3)y=x2-8x+25,9.
【解析】
試題分析:(1)連接OT,根據題意,由勾股定理可得出PT的長;
(2)連接OT,則OP平分劣弧AT,則∠AOP=∠B,從而證出結論;
(3)設PC交⊙O于點D,延長線交⊙O于點E,由相交弦定理,可得出CD的長,再由切割線定理可得出y與x之間的關系式,進而求得y的最小值.
試題解析:(1)連接OT
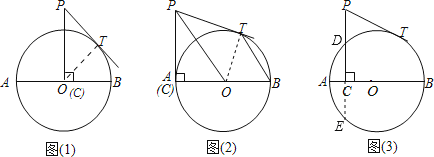
∵PC=5,OT=4,
∴由勾股定理得,PT=![]() ;
;
(2)連接OT,∵PT,PC為⊙O的切線,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT;
(3)設PC交⊙O于點D,延長線交⊙O于點E,
由相交弦定理,得CD2=AC![]() BC,
BC,
∵AC=x,∴BC=8-x,
∴CD=![]() ,
,
∴由切割線定理,得PT2=PD![]() PE,
PE,
∵PT2=y,PC=5,
∴y=[5-![]() ][5+
][5+![]() ],
],
∴y=25-x(8-x)=x2-8x+25,
∴y最小=![]() =9.
=9.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC的頂點A、C、O都在坐標軸上,點B的坐標為(9,4),E為BC邊上一點,CE=6.
(1)求點E的坐標和△ABE的周長;
(2)若P是OA上的一個動點,它以每秒1個單位長度的速度從點O出發沿射線OA運動,設點P運動的時間為t秒(t>0).
①當t為何值時,△PAE的面積等于△PCE的面積的一半;
②當t為何值時,△PAE為直角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】要得到y=﹣2(x+2)2﹣3的圖象,需將拋物線y=﹣2x2作如下平移( )
A. 向右平移2個單位,再向上平移3個單位
B. 向右平移2個單位,再向下平移3個單位
C. 向左平移2個單位,再向上平移3個單位
D. 向左平移2個單位,再向下平移3個單位
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為1,以
的邊長為1,以![]() 為圓心、
為圓心、![]() 為半徑作扇形OA1C1弧A1C1與
為半徑作扇形OA1C1弧A1C1與![]() 相交于點
相交于點![]() ,設正方形
,設正方形![]() 與扇形
與扇形![]() 之間的陰影部分的面積為
之間的陰影部分的面積為![]() ;然后以
;然后以![]() 為對角線作正方形
為對角線作正方形![]() ,又以
,又以![]() 為圓心,、
為圓心,、![]() 為半徑作扇形
為半徑作扇形![]() ,弧A2C2與
,弧A2C2與![]() 相交于點
相交于點![]() ,設正方形
,設正方形![]() 與扇形
與扇形![]() 之間的陰影部分面積為
之間的陰影部分面積為![]() ;按此規律繼續作下去,設正方形
;按此規律繼續作下去,設正方形![]() 與扇形
與扇形![]() 之間的陰影部分面積為
之間的陰影部分面積為![]() .
.
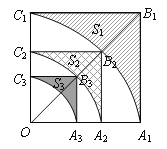
(1)求![]() ;
;
(2)寫出![]() ;
;
(3)試猜想![]() (用含
(用含![]() 的代數式表示,
的代數式表示,![]() 為正整數).
為正整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明為了通過描點法作出函數y=x2-x+1的圖象,先取自變量x的7個值滿足:x2-x1=x3-x2=…=x7-x6=d,再分別算出對應的y值,列出表:

記m1=y2-y1,m2=y3-y2,m3=y4-y3,m4=y5-y4,…;s1=m2-m1,s2=m3-m2,s3=m4-m3,…
(1)判斷s1、s2、s3之間關系,并說明理由;
(2)若將函數“y=x2-x+1”改為“y=ax2+bx+c(a≠0)”,列出表:

其他條件不變,判斷s1、s2、s3之間關系,并說明理由;
(3)小明為了通過描點法作出函數y=ax2+bx+c(a≠0)的圖象,列出表:

由于小明的粗心,表中有一個y值算錯了,請指出算錯的y值(直接寫答案).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com