
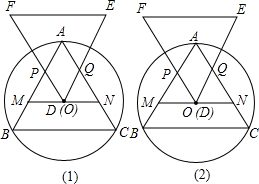
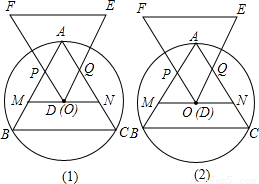
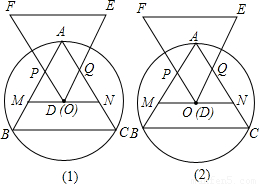
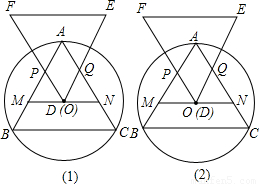
 明理由;你能發現四邊形APDQ的面積與△ABC的面積有何關系嗎?為什么?
明理由;你能發現四邊形APDQ的面積與△ABC的面積有何關系嗎?為什么? x(a-x)=-
x(a-x)=- x2+
x2+ ax=-
ax=- (x-
(x- )2+
)2+ a2
a2 時,即D點位于MN的中點位置時,四邊形APDQ的面積最大,且最大值為
時,即D點位于MN的中點位置時,四邊形APDQ的面積最大,且最大值為 a2.
a2.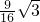 a2,而由(2)知S四邊形APDQ=
a2,而由(2)知S四邊形APDQ= a2
a2 ,
, S△ABC.
S△ABC.

科目:初中數學 來源: 題型:
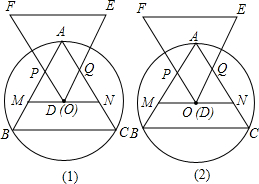 明理由;你能發現四邊形APDQ的面積與△ABC的面積有何關系嗎?為什么?
明理由;你能發現四邊形APDQ的面積與△ABC的面積有何關系嗎?為什么?查看答案和解析>>
科目:初中數學 來源:第34章《二次函數》中考題集(51):34.4 二次函數的應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:第20章《二次函數和反比例函數》中考題集(47):20.5 二次函數的一些應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》中考題集(47):2.4 二次函數的應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2005年山東省濟南市中考數學試卷(課標卷)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com