
【題目】如圖,△AOB是直角三角形,∠AOB=90°,OB=2OA,點A在反比例函數y=![]() 的圖象上.若點B在反比例函數y=
的圖象上.若點B在反比例函數y=![]() 的圖象上,則k的值為_____.
的圖象上,則k的值為_____.

【答案】-4
【解析】
要求函數的解析式只要求出B點的坐標就可以,過點A,B作AC⊥x軸,BD⊥x軸,分別于C,D.根據條件得到△ACO∽△ODB,得到:![]() =2,然后用待定系數法求解即可.
=2,然后用待定系數法求解即可.
過點A,B作AC⊥x軸,BD⊥x軸,分別于C,D,
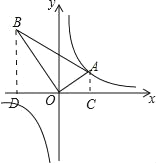
設點A的坐標是(m,n),則AC=n,OC=m.
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA.
∴![]() ,
,
∵OB=2OA,
∴BD=2m,OD=2n,
因為點A在反比例函數y=![]() 的圖象上,
的圖象上,
∴mn=1,
∵點B在反比例函數y=![]() 的圖象上,
的圖象上,
∴B點的坐標是(﹣2n,2m),
∴k=﹣2n2m=﹣4mn=﹣4,
故答案為﹣4.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】有一只拉桿式旅行箱(圖1),其側面示意圖如圖2所示,已知箱體長AB=50cm,拉桿BC的伸長距離最大時可達35cm,點A,B,C在同一條直線上,在箱體底端裝有圓形的滾筒輪⊙A,⊙A與水平地面相切于點D,在拉桿伸長到最大的情況下,當點B距離水平地面34cm時,點C到水平地面的距離CE為55cm.設AF∥ MN.
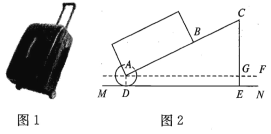
(1)求⊙A的半徑.
(2)當人的手自然下垂拉旅行箱時,人感到較為舒服,某人將手自然下垂在C端拉旅行箱時,CE為76cm,∠CAF=64°,求此時拉桿BC的伸長距離(結果精確到1cm,參考數據:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 兩地相距
兩地相距![]() ,甲、乙兩人從兩地出發相向而行,甲先出發.圖中
,甲、乙兩人從兩地出發相向而行,甲先出發.圖中![]() 表示兩人離
表示兩人離![]() 地的距離
地的距離![]() 與時間
與時間![]() 的關系,結合圖象,下列結論錯誤的是( )
的關系,結合圖象,下列結論錯誤的是( )
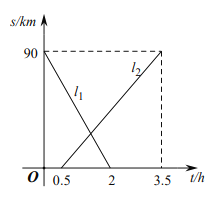
A.![]() 是表示甲離
是表示甲離![]() 地的距離與時間關系的圖象
地的距離與時間關系的圖象
B.乙的速度是![]()
C.兩人相遇時間在![]()
D.當甲到達終點時乙距離終點還有![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個四位數,記千位數字與個位數字之和為![]() ,十位數字與百位數字之和為
,十位數字與百位數字之和為![]() ,如果
,如果![]() ,那么稱這個四位數為“對稱數”
,那么稱這個四位數為“對稱數”
![]() 最小的“對稱數”為 ;四位數
最小的“對稱數”為 ;四位數![]() 與
與![]() 之和為最大的“對稱數”,則
之和為最大的“對稱數”,則![]() 的值為 ;
的值為 ;
![]() 一個四位的“對稱數”
一個四位的“對稱數”![]() ,它的百位數字是千位數字
,它的百位數字是千位數字![]() 的
的![]() 倍,個位數字與十位數字之和為
倍,個位數字與十位數字之和為![]() ,且千位數字
,且千位數字![]() 使得不等式組
使得不等式組 恰有
恰有![]() 個整數解,求出所有滿足條件的“對稱數”
個整數解,求出所有滿足條件的“對稱數”![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是![]() 的直徑,點E是
的直徑,點E是![]() 的中點,CA與
的中點,CA與![]() 相切于點A交BE延長于點C,過點A作
相切于點A交BE延長于點C,過點A作![]() 于點F,交
于點F,交![]() 于點D,交BC于點Q,連接BD.
于點D,交BC于點Q,連接BD.
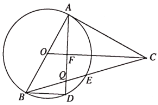
(1)求證:![]() ;
;
(2)若![]() ,求CQ的長.
,求CQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
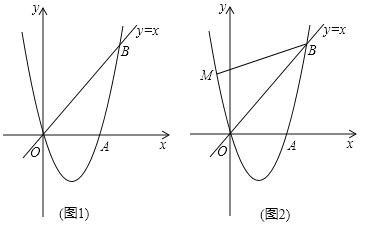
【題目】如圖1,經過原點O的拋物線![]() (a≠0)與x軸交于另一點A(
(a≠0)與x軸交于另一點A(![]() ,0),在第一象限內與直線y=x交于點B(2,t).
,0),在第一象限內與直線y=x交于點B(2,t).
(1)求這條拋物線的表達式;
(2)在第四象限內的拋物線上有一點C,滿足以B,O,C為頂點的三角形的面積為2,求點C的坐標;
(3)如圖2,若點M在這條拋物線上,且∠MBO=∠ABO,在(2)的條件下,是否存在點P,使得△POC∽△MOB?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
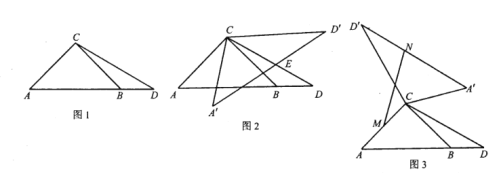
【題目】如圖1,已知![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在
在![]() 邊的延長線上,且
邊的延長線上,且![]() .
.
(1)求![]() 的度數;
的度數;
(2)如圖2,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() (
(![]() )得到
)得到![]() .
.
①若![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,求
,求![]() 的長度;
的長度;
②連接![]() ,
,![]() ,若旋轉過程中
,若旋轉過程中![]() 時,求滿足條件的
時,求滿足條件的![]() 的度數.
的度數.
(3)如圖3,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() (
(![]() )得到
)得到![]() ,若點
,若點![]() 為
為![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 上任意一點,直接寫出旋轉過程中,線段
上任意一點,直接寫出旋轉過程中,線段![]() 長度的取值范圍為______.
長度的取值范圍為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com