
【題目】我們定義:如圖1,在△ABC看,把AB點繞點A順時針旋轉α(0°<α<180°)得到AB',把AC繞點A逆時針旋轉β得到AC',連接B'C'.當α+β=180°時,我們稱△A'B'C'是△ABC的“旋補三角形”,△AB'C'邊B'C'上的中線AD叫做△ABC的“旋補中線”,點A叫做“旋補中心”.
(1)在圖2,圖3中,△AB'C'是△ABC的“旋補三角形”,AD是△ABC的“旋補中線”.①如圖2,當△ABC為等邊三角形時,AD與BC的數量關系為AD=BC;
②如圖3,當∠BAC=90°,BC=8時,則AD長為 .
(2)在圖1中,當△ABC為任意三角形時,猜想AD與BC的數量關系,并給予證明.
(3)如圖4,在四邊形ABCD,∠C=90°,∠D=150°,BC=12,CD=2 ![]() ,DA=6.在四邊形內部是否存在點P,使△PDC是△PAB的“旋補三角形”?若存在,給予證明,并求△PAB的“旋補中線”長;若不存在,說明理由.
,DA=6.在四邊形內部是否存在點P,使△PDC是△PAB的“旋補三角形”?若存在,給予證明,并求△PAB的“旋補中線”長;若不存在,說明理由.
【答案】
(1)![]() ;4
;4
(2)
解:結論:AD= ![]() BC.
BC.
理由:如圖1中,延長AD到M,使得AD=DM,連接E′M,C′M
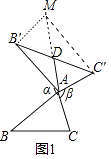
∵B′D=DC′,AD=DM,
∴四邊形AC′MB′是平行四邊形,
∴AC′=B′M=AC,
∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,
∴∠BAC=∠MB′A,∵AB=AB′,
∴△BAC≌△AB′M,
∴BC=AM,
∴AD= ![]() BC
BC
(3)
解:存在.
理由:如圖4中,延長AD交BC的延長線于M,作BE⊥AD于E,作線段BC的垂直平分線交BE于P,交BC于F,連接PA、PD、PC,作△PCD的中線PN.
連接DF交PC于O.
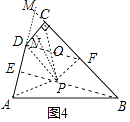
∵∠ADC=150°,
∴∠MDC=30°,
在Rt△DCM中,∵CD=2 ![]() ,∠DCM=90°,∠MDC=30°,
,∠DCM=90°,∠MDC=30°,
∴CM=2,DM=4,∠M=60°,
在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,
∴EM= ![]() BM=7,
BM=7,
∴DE=EM﹣DM=3,
∵AD=6,
∴AE=DE,∵BE⊥AD,
∴PA=PD,PB=PC,
在Rt△CDF中,∵CD=2 ![]() ,CF=6,
,CF=6,
∴tan∠CDF= ![]() ,
,
∴∠CDF=60°=∠CPF,
易證△FCP≌△CFD,
∴CD=PF,∵CD∥PF,
∴四邊形CDPF是矩形,
∴∠CDP=90°,
∴∠ADP=∠ADC﹣∠CDP=60°,
∴△ADP是等邊三角形,
∴∠ADP=60°,∵∠BPF=∠CPF=60°,
∴∠BPC=120°,
∴∠APD+∠BPC=180°,
∴△PDC是△PAB的“旋補三角形”,
在Rt△PDN中,∵∠PDN=90°,PD=AD=6,DN= ![]() ,
,
∴PN= ![]() =
= ![]() =
= ![]()
【解析】解:(1)①如圖2中,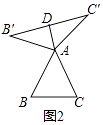
∵△ABC是等邊三角形,
∴AB=BC=AB=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵∠BAC=60°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=120°,
∴∠B′=∠C′=30°,
∴AD= ![]() AB′=
AB′= ![]() BC,
BC,
所以答案是 ![]() .
.
②如圖3中,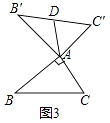
∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD= ![]() B′C′=
B′C′= ![]() BC=4,
BC=4,
所以答案是4.
【考點精析】本題主要考查了直角三角形斜邊上的中線的相關知識點,需要掌握直角三角形斜邊上的中線等于斜邊的一半才能正確解答此題.


 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
【題目】某市政府大力扶持大學生創業.李明在政府的扶持下投資銷售一種進價為每件20元的護眼臺燈,銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數:y=﹣10x+500.
(1)設李明每月獲得利潤為w(元),求出w與x的函數關系式.
(2)如果李明想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
(3)當銷售單價定為多少元時,每月可獲得最大利潤?得最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,拋物線l1:y=ax2﹣4ax+5+4a(a<0)的頂點為A,直線l2:y=kx+3過點A,直線l2與拋物線l1及y軸分別交于B,C.
(1)求k的值;
(2)若B為AC的中點,求a的值;
(3)在(2)的條件下,直接寫出不等式ax2﹣4ax+5+4a<kx+3的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2﹣2 ![]() ax﹣9a與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
ax﹣9a與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
(1)直接寫出a的值、點A的坐標及拋物線的對稱軸;
(2)點P為拋物線的對稱軸上一動點,若△PAD為等腰三角形,求出點P的坐標;
(3)證明:當直線l繞點D旋轉時, ![]() +
+ ![]() 均為定值,并求出該定值.
均為定值,并求出該定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市市民“綠色出行”方式的情況,某校數學興趣小組以問卷調查的形式,隨機調查了某市部分出行市民的主要出行方式(參與問卷調查的市民都只從以下五個種類中選擇一類),并將調查結果繪制成如下不完整的統計圖.
種類 | A | B | C | D | E |
出行方式 | 共享單車 | 步行 | 公交車 | 的士 | 私家車 |

根據以上信息,回答下列問題:
(1)參與本次問卷調查的市民共有人,其中選擇B類的人數有人;
(2)在扇形統計圖中,求A類對應扇形圓心角α的度數,并補全條形統計圖;
(3)該市約有12萬人出行,若將A,B,C這三類出行方式均視為“綠色出行”方式,請估計該市“綠色出行”方式的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P在等邊△ABC的內部,且PC=6,PA=8,PB=10,將線段PC繞點C順時針旋轉60°得到P'C,連接AP',則sin∠PAP'的值為 . 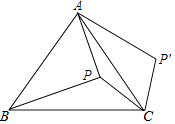
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】植樹節期間,某單位欲購進A、B兩種樹苗,若購進A種樹苗3棵,B種樹苗5顆,需2100元,若購進A種樹苗4顆,B種樹苗10顆,需3800元.
(1)求購進A、B兩種樹苗的單價;
(2)若該單位準備用不多于8000元的錢購進這兩種樹苗共30棵,求A種樹苗至少需購進多少棵?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y= ![]() 與y軸交于點A,與直線y=﹣
與y軸交于點A,與直線y=﹣ ![]() 交于點B,以AB為邊向右作菱形ABCD,點C恰與原點O重合,拋物線y=(x﹣h)2+k的頂點在直線y=﹣
交于點B,以AB為邊向右作菱形ABCD,點C恰與原點O重合,拋物線y=(x﹣h)2+k的頂點在直線y=﹣ ![]() 上移動.若拋物線與菱形的邊AB、BC都有公共點,則h的取值范圍是( )
上移動.若拋物線與菱形的邊AB、BC都有公共點,則h的取值范圍是( )
A.﹣2 ![]()
B.﹣2≤h≤1
C.﹣1 ![]()
D.﹣1 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著柴靜紀錄片《穹頂之下》的播出,全社會對空氣污染問題越來越重視,空氣凈化器的銷量也大增,商社電器從廠家購進了A,B兩種型號的空氣凈化器,已知一臺A型空氣凈化器的進價比一臺B型空氣凈化器的進價多300元,用7500元購進A型空氣凈化器和用6000元購進B型空氣凈化器的臺數相同.
(1)求一臺A型空氣凈化器和一臺B型空氣凈化器的進價各為多少元?
(2)在銷售過程中,A型空氣凈化器因為凈化能力強,噪音小而更受消費者的歡迎.為了增大B型空氣凈化器的銷量,商社電器決定對B型空氣凈化器進行降價銷售,經市場調查,當B型空氣凈化器的售價為1800元時,每天可賣出4臺,在此基礎上,售價每降低50元,每天將多售出1臺,如果每天商社電器銷售B型空氣凈化器的利潤為3200元,請問商社電器應將B型空氣凈化器的售價定為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com