
(12分)如圖,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒1㎝,設出發的時間為t秒.
(1)出發2秒后,求△ABP的周長。
(2)問t為何值時,△BCP是以BC為腰的等腰三角形?
(3)另有一點Q,從點C開始,按C→B→A→C的路徑運動,且速度為每秒2㎝,若P、Q兩點同時出發,當P、Q中有一點到達終點時,另一點也停止運動。當t為何值時,直線PQ把△ABC的周長分成相等的兩部分?
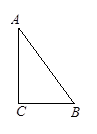
 (1)當t=2時,CP=2, 1分
(1)當t=2時,CP=2, 1分
在Rt△BCA中,由勾股定理得
AC=4
∴AP=2 1分
在Rt△BCP中,由勾股定理得
∴![]() 1分
1分
∴△ABP的周長=2+5+![]() =
=![]() 1分
1分
(2)①BC=CP=3cm,有兩種情況:
i)若P在邊AC上時,
此時t=3s,△BCP為等腰三角形; 1分
ii)若P在AB邊上時,CP=BC=3cm,過C作斜邊AB的高,根據面積法求得高為2.4cm, 1分
根據勾股定理可求得BP=3.6cm,
所以P運動的路程為9-3.6=5.4cm,
則用的時間為5.4s,△BCP為等腰三角形 1分
②BP=CB=3cm,
此時AP=2cm,P運動的路程為2+4=6cm, 1分
(3)由題可知P運動的路程為t, Q運動的路程為2t,
要使PQ把△ABC的周長平均分成兩份,所以P、Q運動的路程和為6或者比12多6。
∴2t+t=6或2t+t=12+6 2分
∴t=2 或t=6 2分
解析:略


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 ,求此時直線PM的解析式;
,求此時直線PM的解析式;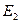 ,PM的延長線與CD的延長線交于點F,若三角形G
,PM的延長線與CD的延長線交于點F,若三角形G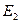 F的面積為4,求此時直線PM的解析式;
F的面積為4,求此時直線PM的解析式;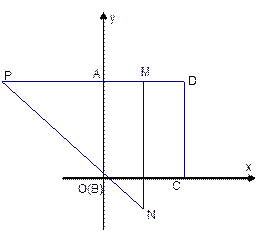
查看答案和解析>>
科目:初中數學 來源:2012-2013學年浙江省杭州市九年級12月月考數學試卷(解析版) 題型:解答題
(本題12分)如圖,二次函數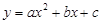 的圖象與x軸交于兩個不同的點A(-2,0)、B(4,0),與y軸交于點C(0,3),連結BC、AC,該二次函數圖象的對稱軸與x軸相交于點D.
的圖象與x軸交于兩個不同的點A(-2,0)、B(4,0),與y軸交于點C(0,3),連結BC、AC,該二次函數圖象的對稱軸與x軸相交于點D.
(1)求這個二次函數的解析式、點D的坐標及直線BC的函數解析式;
(2)點Q在線段BC上,使得以點Q、D、B為頂點的三角形與△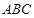 相似,求出點Q的坐標;
相似,求出點Q的坐標;
(3)在(2)的條件下,若存在點Q,請任選一個Q點求出△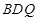 外接圓圓心的坐標.
外接圓圓心的坐標.

查看答案和解析>>
科目:初中數學 來源:2011-2012年浙江省九年級12月月考數學卷 題型:解答題
(本題12分)如圖,拋物線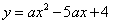 經過
經過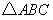 的三個頂點,已知
的三個頂點,已知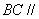
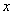 軸,點
軸,點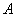 在
在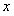 軸上,點
軸上,點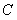 在
在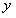 軸上,且
軸上,且 .
.
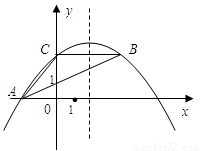
1.(1)求拋物線的對稱軸;
2.(2)寫出A,B,C三點的坐標(A,B,C三點的坐標只需寫出答案),并求拋物線的解析式;
3.(3)探究:若點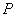 是拋物線對稱軸上且在
是拋物線對稱軸上且在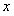 軸下方的動點,是否存在
軸下方的動點,是否存在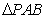 是等腰三角形.若存在,求出所有符合條件的點
是等腰三角形.若存在,求出所有符合條件的點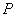 坐標;不存在,請說明理由.
坐標;不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2011年初中畢業升學考試(廣東佛山卷)數學 題型:解答題
(2011內蒙古赤峰,22,
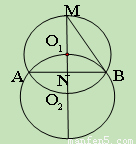
12分)如圖,等圓⊙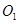 和⊙
和⊙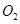 相交于A、B兩點,⊙
相交于A、B兩點,⊙
(1)求證:BM是⊙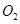 的切線;
的切線;
(2)求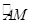 的長。
的長。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com