
【題目】如圖,在△ABC中,CD是AB邊上的中線,E是CD的中點,過點C作AB的平行線交AE的延長線于點F,連接BF.
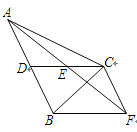
(1) 求證:CF=AD;
(2) 若CA=CB,∠ACB=90°,試判斷四邊形CDBF的形狀,并說明理由.
【答案】見解析;正方形.
【解析】
試題(1)、根據CF∥AB可得∠CFE=∠DAE,∠FCE=∠ADE,根據E為中點可得CE=DE,則△ECF和△DEA全等,從而得出答案;(2)、根據AD=BD,則CF=BD,CF∥BD得出平行四邊形,根據CD為AB邊上的中線,CA=CB得出∠BDC=90°得出矩形,根據CD為等腰直角△ABC斜邊上的中線得出CD=BD,即得到正方形.
試題解析:(1)、∵CF∥AB,∴∠CFE=∠DAE,∠FCE=∠ADE,∵E為CD的中點,∴CE=DE,
∴△ECF≌△DEA(AAS), ∴CF=AD,
(2)四邊形CDBF為正方形,理由為:
∵AD=BD, ∴CF=BD; ∵CF=BD,CF∥BD,∴四邊形CDBF為平行四邊形,
∵CA=CB,CD為AB邊上的中線,∴CD⊥AB,即∠BDC=90°,∴四邊形CDBF為矩形,
∵等腰直角△ABC中,CD為斜邊上的中線,∴CD=![]() AB,即CD=BD,則四邊形CDBF為正方形.
AB,即CD=BD,則四邊形CDBF為正方形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
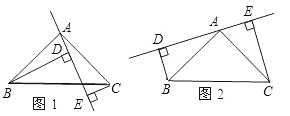
【題目】如圖1,△ABC中,AB=AC,∠BAC=90°,直線l經過點A,過B、C兩點分別作直線l的垂線段,垂足分別為D、E.
(1)如圖1,△ABD與與△CAE全等嗎?請說明理由;
(2)如圖1,BD=DE+CE成立嗎?為什么?
(3)若直線AE繞A點旋轉到如圖2位置時,其它條件不變,BD與DE、CE關系如何?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為深化義務教育課程改革,滿足學生的個性化學習需求,某校就“學生對知識拓展、體育特長、藝術特長和時間活動四類選課意向”進行了抽樣調查(每人選報一類),繪制了如圖所示的兩幅統計圖(不完整),請根據圖中信息,解答下列問題.
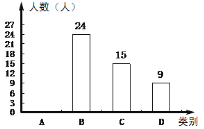
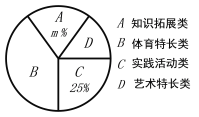
(1)求扇形統計圖中的m的值,并補全條形統計圖;
(2)已知該校800名學生,計劃開設“實踐活動類”課程,每班安排20人,問學校開設多少個“實踐活動課”課程的班級比較合理.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“趙爽弦圖”巧妙地利用面積關系證明了勾股定理,是我國古代數學的驕傲,如圖所示“趙爽弦圖”是由四個全等的直角三角形和一個小正方形拼成的一個大正方形,設直角三角形較長直角邊長為a,較短直角邊長為b,若(a+b)2=21,大正方形的面積為13,則小正方形的面積為
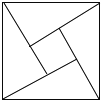
A. 3B. 4C. 5D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】本商場為了吸引顧客,設立了一個可以自由轉動的轉盤,如圖所示,并規定,顧客消費100元以上(不包括100元),就能獲得一次轉動轉盤的機會,如果轉盤停止后,指針正好對準打折區域顧客就可以獲得此項待遇(轉盤等分成8份,指針停在每個區域的機會相等).
(1)顧客小華消費150元,獲得打折待遇的概率是多少?
(2)顧客小明消費120元,獲得五折待遇的概率是多少?
(3)小華對小明說:“我們用這個轉盤來做一個游戲,指針指到五折你贏,指針指到七折算我贏”,你認為這個游戲規則公平嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中每個小方格的邊長為1,且點A,B,C均為格點.

(1)畫出△ABC關于直線l的對稱圖形△A1B1C1;
(2)求△ABC的面積;
(3)邊AB=_____________(不用寫過程);
(4)在直線l上找一點D,使AD+BD最小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如圖所示的方式放置,其中點B1在y軸上,點C1、E1、E2、C2、E3、E4、C3……在x軸上,已知正方形A1B1C1D1的邊長為l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,則正方形A2017B2017 C2017 D2017的邊長是( )

A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E在邊CD上,將該矩形沿AE折疊,使點D落在邊BC上的點F處,過點F作FG∥CD,交AE于點G,連接DG.

(1)求證:四邊形DEFG為菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
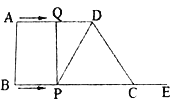
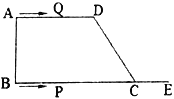
【題目】如圖四邊形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .動點
.動點![]() 從點
從點![]() 出發,沿射線
出發,沿射線![]() 的方向以每秒
的方向以每秒![]() 的速度運動到
的速度運動到![]() 點返回,動點
點返回,動點![]() 從點
從點![]() 出發,在線段
出發,在線段![]() 上以每秒
上以每秒![]() 的速度向點
的速度向點![]() 運動,點
運動,點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時出發,當點
同時出發,當點![]() 運動到點
運動到點![]() 時,點
時,點![]() 停止運動,設運動時間為
停止運動,設運動時間為![]() (秒).
(秒).


(1)當![]() 時,是否存在點
時,是否存在點![]() ,使四邊形
,使四邊形![]() 是平行四邊形,若存在,求出
是平行四邊形,若存在,求出![]() 值;若不存在,請說明理由;
值;若不存在,請說明理由;
(2)當![]() 為何值時,以
為何值時,以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形面積等于
為頂點的四邊形面積等于![]() ;
;
(3)當![]() 時,是否存在點
時,是否存在點![]() ,使
,使![]() 是等腰三角形?若存在,請直接寫出所有滿足要求的
是等腰三角形?若存在,請直接寫出所有滿足要求的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com