Question

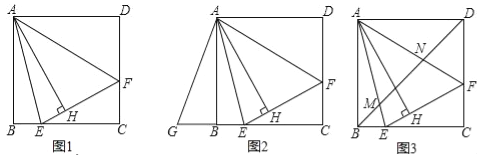
【題目】如圖1，在正方形ABCD內作∠EAF=45°，AE交BC于點E，AF交CD于點F，連接EF，過點A作AH⊥EF，垂足為H．

（1）如圖2，將△ADF繞點A順時針旋轉90°得到△ABG．

①求證：△AGE≌△AFE；

②若BE=2，DF=3，求AH的長．

（2）如圖3，連接BD交AE于點M，交AF于點N．請探究并猜想：線段BM，MN，ND之間有什么數量關系？并說明理由．

Answer 1

【答案】（1）①詳見解析；②6；（2）MN2=ND2+BM2,，理由見解析.

【解析】

試題分析：（1）①由旋轉的性質可知：AF=AG，∠DAF=∠BAG，接下來在證明∠GAE=∠FAE，然后依據SAS證明△GAE≌△FAE即可；②由全等三角形的性質可知：AB=AH，GE=EF=5．設正方形的邊長為x，在Rt△EFC中，依據勾股定理列方程求解即可；（2）將△ABM逆時針旋轉90°得△ADM′．在△NM′D中依據勾股定理可證明NM′2=ND2+DM′2，接下來證明△AMN≌△ANM′，于的得到MN=NM′，最后再由BM=DM′證明即可．

試題解析：（1）①由旋轉的性質可知：AF=AG，∠DAF=∠BAG．

∵四邊形ABCD為正方形，

∴∠BAD=90°．

又∵∠EAF=45°，

∴∠BAE+∠DAF=45°．

∴∠BAG+∠BAE=45°．

∴∠GAE=∠FAE．

在△GAE和△FAE中，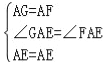

∴△GAE≌△FAE．

②∵△GAE≌△FAE，AB⊥GE，AH⊥EF，

∴AB=AH，GE=EF=5．

設正方形的邊長為x，則EC=x﹣2，FC=x﹣3．

在Rt△EFC中，由勾股定理得：EF2=FC2+EC2，即（x﹣2）2+（x﹣3）2=25．

解得：x=6．

∴AB=6．

∴AH=6．

（3）如圖所示：將△ABM逆時針旋轉90°得△ADM′．

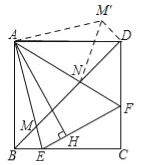
∵四邊形ABCD為正方形，

∴∠ABD=∠ADB=45°．

由旋轉的性質可知：∠ABM=∠ADM′=45°，BE=DM′．

∴∠NDM′=90°．

∴NM′2=ND2+DM′2．

∵∠EAM′=90°，∠EAF=45°，

∴∠EAF=∠FAM′=45°．

在△AMN和△ANM′中，，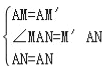

∴△AMN≌△ANM′．

∴MN=NM′．

又∵BM=DM′，

∴MN2=ND2+BM2．