
定義:我們把三角形被一邊中線分成的兩個三角形叫做“友好三角形”.
性質:如果兩個三角形是“友好三角形”,那么這兩個三角形的面積相等.
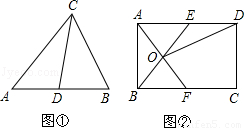
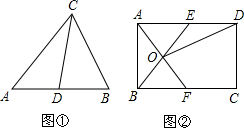
理解:如圖①,在△ABC中,CD是AB邊上的中線,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
應用:如圖②,在矩形ABCD中,AB=4,BC=6,點E在AD上,點F在BC上,AE=BF,AF與BE交于點O.
(1)求證:△AOB和△AOE是“友好三角形”;
(2)連接OD,若△AOE和△DOE是“友好三角形”,求四邊形CDOF的面積.
探究:在△ABC中,∠A=30°,AB=4,點D在線段AB上,連接CD,△ACD和△BCD是“友好三角形”,將△ACD沿CD所在直線翻折,得到△A′CD,若△A′CD與△ABC重合部分的面積等于△ABC面積的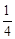 ,請直接寫出△ABC的面積.
,請直接寫出△ABC的面積.
應用:(1)證明見解析
(2)△ABC的面積是2或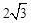 。
。
【解析】
試題分析:應用:(1)連接EF,根據一組對邊平行且相等的四邊形是平行四邊形,得到四邊形ABFE是平行四邊形,從而根據平行四邊形的性質證得OE=OB,即可證得△AOE和△AOB是友好三角形。
(2)△AOE和△DOE是“友好三角形”,即可得到E是AD的中點,則可以求得△ABE、△ABF的面積,根據S四邊形CDOF=S矩形ABCD﹣2S△ABF即可求解。
解:應用:(1)證明:如圖,連接EF,
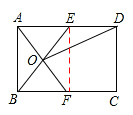
∵四邊形ABCD是矩形,
∴AD∥BC。
∵AE=BF,∴四邊形ABFE是平行四邊形。
∴OE=OB。∴△AOE和△AOB是友好三角形。
探究:分為兩種情況:
①如圖1,連接A′B,過B作BM⊥AC于M,
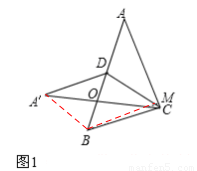
∵S△ACD=S△BCD.∴AD=BD=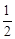 AB。
AB。
∵沿CD折疊A和A′重合,∴AD=A′D=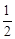 AB=
AB=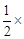 4=2。
4=2。
∵△A′CD與△ABC重合部分的面積等于△ABC面積的 ,
,
∴S△DOC= S△ABC=
S△ABC=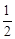 S△BDC=
S△BDC=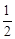 S△ADC=
S△ADC=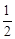 S△A′DC。
S△A′DC。
∴DO=OB,A′O=CO。∴四邊形A′DCB是平行四邊形。∴BC=A′D=2。
∵AB=4,∠BAC=30°,∴BM=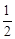 AB=2=BC。
AB=2=BC。
∴C和M重合。∴∠ACB=90°。
由勾股定理得: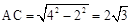 ,
,
∴△ABC的面積是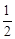 ×BC×AC=
×BC×AC=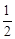 ×2×
×2×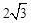 =
=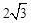 。
。
②如圖2,連接A′B,過C作CQ⊥A′D于Q,

∵S△ACD=S△BCD,∴AD=BD=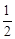 AB。
AB。
∵沿CD折疊A和A′重合,∴AD=A′D=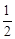 AB
AB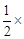 4=2。
4=2。
∵△A′CD與△ABC重合部分的面積等于△ABC面積的 ,
,
∴S△DOC= S△ABC=
S△ABC=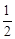 S△BDC=
S△BDC=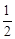 S△ADC=
S△ADC=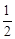 S△A′DC,
S△A′DC,
∴DO=OA′,BO=CO。∴四邊形A′DCB是平行四邊形。
∴BD=A′C=2。
∵A′C=2,∠DA′C=∠BAC=30°,∴CQ=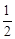 A′C=1,
A′C=1,
∴S△ABC=2S△ADC=2S△A′DC=2×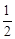 ×A′D×CQ=2×
×A′D×CQ=2×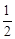 ×2×1=2。
×2×1=2。
綜上所述,△ABC的面積是2或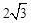 。
。


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
 (2013•沈陽)定義:我們把三角形被一邊中線分成的兩個三角形叫做“友好三角形”.
(2013•沈陽)定義:我們把三角形被一邊中線分成的兩個三角形叫做“友好三角形”.| 1 | 4 |
查看答案和解析>>
科目:初中數學 來源:2013年遼寧省遼陽市高級中等學校招生考試數學 題型:044
定義:我們把三角形被一邊中線分成的兩個三角形叫做“友好三角形”
性質:如果兩個三角形是“友好三角形”,那么這兩個三角形的面積相等,
理解:如圖①,在△ABC中,CD是AB邊上的中線,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.

應用:如圖②,在矩形ABCD中,AB=4,BC=6,點E在AD上,點F在BC上,AE=BF,AF與BE交于點O,

(1)求證:△AOB和△AOE是“友好三角形”;
(2)連接OD,若△AOE和△DOE是“友好三角形”,求四邊形CDOF的面積,
探究:在△ABC中,∠A=30°,AB=4,點D在線段AB上,連接CD,△ACD和△BCD是“友好三角形”,將△ACD沿CD所在直線翻折,得到△![]() CD與△ABC重合部分的面積等于△ABC面積的
CD與△ABC重合部分的面積等于△ABC面積的![]() ,請直接寫出△ABC的面積.
,請直接寫出△ABC的面積.
查看答案和解析>>
科目:初中數學 來源:2013年遼寧省沈陽市中考數學試卷(解析版) 題型:解答題
 ,請直接寫出△ABC的面積.
,請直接寫出△ABC的面積.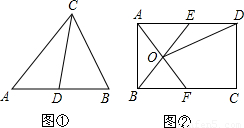
查看答案和解析>>
科目:初中數學 來源: 題型:
定義:我們把三![]() 角形被一邊中線分成的兩個三角形叫做“友好三角形”
角形被一邊中線分成的兩個三角形叫做“友好三角形”
性質:如果兩個三角形是“友好三角形”,那么這兩個三角形的面積相等,
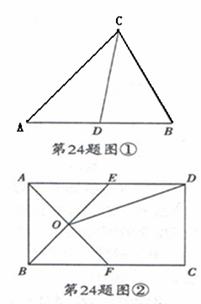
理解:如圖①,在![]() 中,CD是AB邊上的中線,那么
中,CD是AB邊上的中線,那么![]() 和
和![]() 是“友好三角形”,并且
是“友好三角形”,并且![]() 。
。
應用:如圖②,在矩形ABCD中,AB=4,BC=6,點E在AD上,點F在BC上,AE=BF,AF與BE交于點O,
(1) 求證: ![]() 和
和![]() 是“友好三角形”;
是“友好三角形”;
(2) 連接OD,若![]() 和
和![]() 是“友好三角形”,求四邊形CDOF的面積,
是“友好三角形”,求四邊形CDOF的面積,
探究:在![]() 中,
中,![]() ,AB=4,點D在線段AB上,連接CD,
,AB=4,點D在線段AB上,連接CD,![]() 和
和![]() 是“友好三角形”,將
是“友好三角形”,將![]() 沿CD所在直線翻折,得到
沿CD所在直線翻折,得到![]() 與
與![]() 重合部分的面積等于
重合部分的面積等于![]() 面積的
面積的![]() ,請直接寫出
,請直接寫出![]() 的面積。
的面積。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com