
【題目】如圖,在平面直角坐標系中,拋物線![]() 交x軸于A,B兩點,交y軸于點C(0,3),tan∠OAC=
交x軸于A,B兩點,交y軸于點C(0,3),tan∠OAC=![]() .
.
(1)求拋物線的解析式;
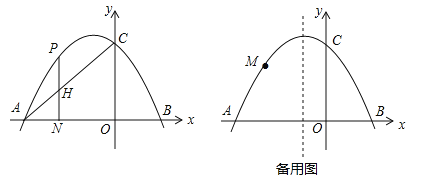
(2)點H是線段AC上任意一點,過H作直線HN⊥x軸于點N,交拋物線于點P,求線段PH的最大值;
(3)點M是拋物線上任意一點,連接CM,以CM為邊作正方形CMEF,是否存在點M使點E恰好落在對稱軸上?若存在,請求出點M的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)M(﹣4,0)或(
;(3)M(﹣4,0)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(2,0).
)或(2,0).
【解析】
試題分析:(1)由點C的坐標以及tan∠OAC=![]() 可得出點A的坐標,結合點A、C的坐標利用待定系數法即可求出拋物線的解析式;
可得出點A的坐標,結合點A、C的坐標利用待定系數法即可求出拋物線的解析式;
(2)設直線AC的解析式為y=kx+b,由點A、C的解析式利用待定系數法即可求出直線AC的解析式,設N(x,0)(﹣4<x<0),可找出H、P的坐標,由此即可得出PH關于x的解析式,利用配方法即二次函數的性質即可解決最值問題;
(3)過點M作MK⊥y軸于點K,交對稱軸于點G,根據角的計算依據正方形的性質即可得出△MCK≌△MEG(AAS),進而得出MG=CK.設出點M的坐標利用正方形的性質即可得出點G、K的坐標,由正方形的性質即可得出關于x的含絕對值符號的一元二次方程,解方程即可求出x值,將其代入拋物線解析式中即可求出點M的坐標.
試題解析:(1)∵C(0,3),∴OC=3,∵tan∠OAC=![]() ,∴OA=4,∴A(﹣4,0).
,∴OA=4,∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入![]() 中,得:
中,得:![]() ,解得:
,解得: ,∴拋物線的解析式為
,∴拋物線的解析式為![]() .
.
(2)設直線AC的解析式為y=kx+b,把A(﹣4,0)、C(0,3)代入y=kx+b中,得:![]() ,解得:
,解得:![]() ,∴直線AC的解析式為
,∴直線AC的解析式為![]() .
.
設N(x,0)(﹣4<x<0),則H(x,![]() ),P(x,
),P(x,![]() ),∴PH=
),∴PH=![]() =
=![]() =
=![]() ,∵
,∵![]() <0,∴PH有最大值,當x=2時,PH取最大值,最大值為
<0,∴PH有最大值,當x=2時,PH取最大值,最大值為![]() .
.
(3)過點M作MK⊥y軸于點K,交對稱軸于點G,則∠MGE=∠MKC=90°,∴∠MEG+∠EMG=90°,∵四邊形CMEF是正方形,∴EM=MC,∠MEC=90°,∴∠EMG+∠CMK=90°,∴∠MEG=∠CMK.
在△MCK和△MEG中,∵∠MEG=∠CMK,∠MGE=∠CKM,EM=MC,∴△MCK≌△MEG(AAS),∴MG=CK.
由拋物線的對稱軸為x=﹣1,設M(x,![]() ),則G(﹣1,
),則G(﹣1,![]() ),K(0,
),K(0,![]() ),∴MG=|x+1|,CK=|
),∴MG=|x+1|,CK=|![]() |=|
|=|![]() |=|
|=|![]() |,∴|x+1|=|
|,∴|x+1|=|![]() |,∴
|,∴![]() =±(x+1),解得:x1=﹣4,x2=
=±(x+1),解得:x1=﹣4,x2=![]() ,x3=
,x3=![]() ,x4=2,代入拋物線解析式得:y1=0,y2=
,x4=2,代入拋物線解析式得:y1=0,y2=![]() ,y3=
,y3=![]() ,y4=0,∴點M的坐標是(﹣4,0),(
,y4=0,∴點M的坐標是(﹣4,0),(![]() ,
,![]() ),(
),(![]() ,
,![]() )或(2,0).
)或(2,0).



科目:初中數學 來源: 題型:
【題目】如圖,已知點C是線段AB的中點,點D是線段AC的中點,點E是線段BC的中點.![]()
(1)若線段DE=11cm,求線段AB的長.
(2)若線段CE=4cm,求線段DB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C在線段AB上,AC=8 cm,CB=6 cm,點M,N分別是AC,BC的中點.![]()
(1)求線段MN的長.
(2)若C為線段AB上任一點,滿足AC+CB=a cm,其他條件不變,你能猜想MN的長度嗎?(用含a的代數式表示)并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A.沒有最大的正數,卻有最大的負整數
B.數軸上離原點越遠,表示數越大
C.0大于一切非負數
D.在原點左邊離原點越遠,數就越小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△A′B′C′關于直線l對稱,求證:△ABC≌△A′B′C′.若△ABC≌△A′B′C′,那么△ABC和△A′B′C′一定關于某條直線l對稱嗎?若一定請給出證明,若不一定請畫出反例圖。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,真命題有( )
①鄰補角的角平分線互相垂直;②兩條直線被第三條直線所截,內錯角相等;③兩邊分別平行的兩角相等;④如果x2>0,那么x>0;⑤經過直線外一點,有且只有一條直線與這條直線平行.
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC為等邊三角形,AE=CD,AD、BE相交于點P,BQ⊥AD于點Q,PQ=4,PE=1. 
(1)求∠BPQ的度數;
(2)求AD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com