
 如圖:已知在△ABC中,AB=AC,D、E、F分別為AB、BC、CA上的中點.
如圖:已知在△ABC中,AB=AC,D、E、F分別為AB、BC、CA上的中點.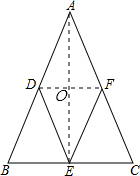 (1)證明:∵D、E、F分別為AB、BC、CA上的中點.
(1)證明:∵D、E、F分別為AB、BC、CA上的中點.
 AC,EF
AC,EF
 AB,
AB, AE,OD=
AE,OD= DF.
DF. AB=
AB= ,DF=
,DF= BC=5,
BC=5,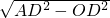 =
= =6,
=6, DF•AE=
DF•AE= 5×12=30,即四邊形ADEF的面積是30.
5×12=30,即四邊形ADEF的面積是30.

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com