
【題目】萬安縣開發區某電子電路板廠到井岡山大學從應屆畢業生中招聘公司職員,對應聘者的專業知識、英語水平、參加社會實踐與社團活動等三項進行測試或成果認定,三項的得分滿分都為100分,三項的分數分別按5∶3∶2的比例記入每人的最后總分,有4位應聘者的得分如下表所示.
| 專業知識 | 英語水平 | 參加社會實踐與 社團活動等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分別算出4位應聘者的總分;
(2)表中四人“專業知識”的平均分為85分,方差為12.5,四人“英語水平”的平均分為87.5分,方差為6.25,請你求出四人“參加社會實踐與社團活動等”的平均分及方差;
(3)分析(1)和(2)中的有關數據,你對大學生應聘者有何建議?
【答案】(1)應聘者甲總分為86分;應聘者乙總分為82分;應聘者丙總分為81分;應聘者丁總分為82分.(2)200;(3)詳見解析.
【解析】
(1) 根據加權平均數的計算公式列出算式, 再進行計算即可.
(2) 平均數為一組數據中所有數據之和再除以這組數據的個數.根據平均數的計算公式先算出平均數, 再根據方差公式進行計算即可.
(3) 根據 (1) 、 (2) 得出的結論和實際情況分別寫出合理的建議即可.
解:(1)應聘者甲總分為86分;應聘者乙總分為82分;
應聘者丙總分為81分;應聘者丁總分為82分.
(2)4人參加社會實踐與社團活動等的平均分數:![]()
方差:![]()
![]()
(3)對于應聘者的專業知識、英語水平的差距不大,但參加社會實踐與社團活動等方面的差距較大,影響學生的最后成績,將影響學生就業.學生不僅注重自己的文化知識的學習,更應注重社會實踐與社團活動的開展,從而促進學生綜合素質的提升.


科目:初中數學 來源: 題型:
【題目】如圖,點P是∠AOB外的一點,點Q是點P關于OA的對稱點,點R是點P關于OB的對稱點,直線QR分別交∠AOB兩邊OA,OB于點M,N,連結PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,D是邊AC上的一點,連接BD,使∠A=2∠1,E是BC上的一點,以BE為直徑的⊙O經過點D. 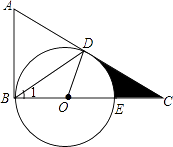
(1)求證:AC是⊙O的切線;
(2)若∠A=60°,⊙O的半徑為2,求陰影部分的面積.(結果保留根號和π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線BD經過坐標原點,矩形的邊分別平行于坐標軸,點C在反比例函數 ![]() 的圖象上.若點A的坐標為(﹣2,﹣2),則k的值為 .
的圖象上.若點A的坐標為(﹣2,﹣2),則k的值為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面內的兩條直線有相交和平行兩種位置關系.
(1)如圖1,若AB∥CD,點P在AB、CD內部,∠B=50°,∠D=30°,求∠BPD.
(2)如圖2,將點P移到AB、CD外部,則∠BPD、∠B、∠D之間有何數量關系?(不需證明)
(3)如圖3,寫出∠BPD﹑∠B﹑∠D﹑∠BQD之間的數量關系?請證明你的結論.
(4)如圖4,求出∠A+∠B+∠C+∠D+∠E+∠F的度數.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知y=﹣x+m(m>4)過動點A(m,0),并與反比例函數y= ![]() 的圖象交于B、C兩點(點B在點C的左邊),以OA為直徑作反比例函數y=
的圖象交于B、C兩點(點B在點C的左邊),以OA為直徑作反比例函數y= ![]() 的圖象相交的半圓,圓心為P,過點B作x軸的垂線,垂足為E,并于半圓P交于點D.
的圖象相交的半圓,圓心為P,過點B作x軸的垂線,垂足為E,并于半圓P交于點D. 
(1)當m=5時,求B、C兩點的坐標.
(2)求證:無論m取何值,線段DE的長始終為定值.
(3)記點C關于直線DE的對稱點為C′,當四邊形CDC′E為菱形時,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中AB=3,BC=4,∠B=90°,點B、C在兩坐標軸上滑動.當邊AC⊥x軸時,點A剛好在雙曲線 ![]() 上,此時下列結論不正確的是( )
上,此時下列結論不正確的是( )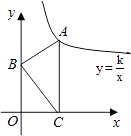
A.點B為(0, ![]() )
)
B.AC邊的高為 ![]()
C.雙曲線為 ![]()
D.此時點A與點O距離最大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過原點o和x軸上一點A(4,0),拋物線頂點為E,它的對稱軸與x軸交于點D.直線y=﹣2x﹣1經過拋物線上一點B(﹣2,m)且與y軸交于點C,與拋物線的對稱軸交于點F.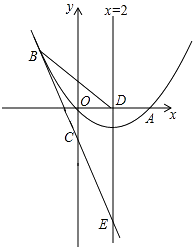
(1)求m的值及該拋物線對應的解析式;
(2)P(x,y)是拋物線上的一點,若S△ADP=S△ADC , 求出所有符合條件的點P的坐標;
(3)點Q是平面內任意一點,點M從點F出發,沿對稱軸向上以每秒1個單位長度的速度勻速運動,設點M的運動時間為t秒,是否能使以Q、A、E、M四點為頂點的四邊形是菱形.若能,請直接寫出點M的運動時間t的值;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com