
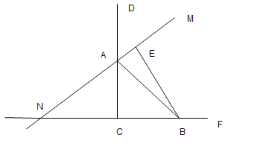
【題目】如圖正方形![]() 的頂點
的頂點![]() 是
是![]() 和
和![]() 上的動點,與
上的動點,與![]() 交于P、Q兩點,
交于P、Q兩點,![]() .
.
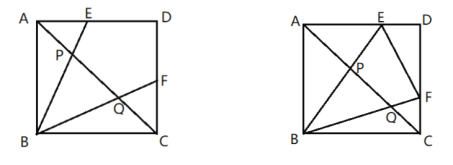
(1)當![]() 時,
時,
①求![]() 的度數;
的度數;
②求以![]() 為邊長的正方形面積;
為邊長的正方形面積;
(2)當![]() 在
在![]() 上運動時,始終保持
上運動時,始終保持![]() ,連接
,連接![]() ,則
,則![]() 面積的最小值為 (直接寫出答案).
面積的最小值為 (直接寫出答案).
【答案】(1)①![]() ,②以
,②以![]() 為邊的正方形面積為
為邊的正方形面積為![]() ;(2)
;(2)![]() .
.
【解析】
(1)根據正方形性質得出![]() ,
,![]() ,由此得知
,由此得知![]() ,然后根據AB=AQ=CP,結合等腰三角形性質以及三角形內角和定理進一步求出答案即可;
,然后根據AB=AQ=CP,結合等腰三角形性質以及三角形內角和定理進一步求出答案即可;
(2)首先根據勾股定理求出![]() ,由此得出
,由此得出![]() ,通過證明
,通過證明![]() 進一步得出
進一步得出![]() ,據此即可得出答案;
,據此即可得出答案;
(3)延長![]() 至點
至點![]() ,使
,使![]() ,連接
,連接![]() ,先證明
,先證明![]() 與
與![]() 全等,得出∠GBF=∠EBF,再證明
全等,得出∠GBF=∠EBF,再證明![]() 與
與![]() 全等,從而得出
全等,從而得出![]() ,即當
,即當![]() 時,
時,![]() 取得最小值,設此時
取得最小值,設此時![]() ,則
,則![]() ,根據題意利用勾股定理得出
,根據題意利用勾股定理得出![]() ,最后得出
,最后得出![]() ,
,![]() ,據此進一步求解即可.
,據此進一步求解即可.
(1)①∵四邊形![]() 為正方形,
為正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵AB=AQ=CP,
∴AB=AQ=CP=BC,
∴![]() ,
,
同理![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
故以![]() 為邊的正方形面積為
為邊的正方形面積為![]() ;
;
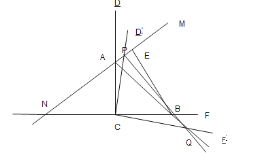
(2)如圖,延長![]() 至點
至點![]() ,使
,使![]() ,連接
,連接![]() ,
,
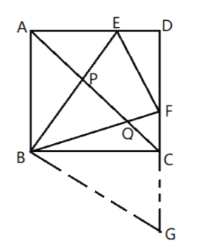
在![]() 與
與![]() 中,
中,
∵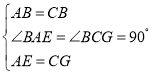
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴∠GBF=∠EBF,
在![]() 與
與![]() 中,
中,
∵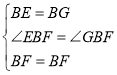
∴![]()
∴![]() ,
,
在![]() 中,
中,![]() ,
,
當且僅當![]() 時等號成立,此時
時等號成立,此時![]() ,
,
設此時![]() ,則
,則![]() ,
,
![]()
由![]() 得:
得:![]()
即![]()
解得![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,
∴![]() 面積的最小值=
面積的最小值=![]() ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】有紅、黃兩個布袋,紅布袋中有兩個完全相同的小球,分別標有數字2和4.黃布袋中有三個完全相同的小球,分別標有數字﹣2,﹣4和﹣6.小賢先從紅布袋中隨機取出一個小球,記錄其標有的數字為x,再從黃布袋中隨機取出一個小球,記錄其標有的數字為y,這樣就確定點M的一個坐標為(x.y)
(1)用列表或畫樹狀圖的方法寫出點M的所有可能坐標;
(2)求點M落在雙曲線y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 是
是![]() 外角
外角![]() 的角平分線,反向延長
的角平分線,反向延長![]() 與線段
與線段![]() 延長線交于點
延長線交于點![]() 過
過![]() 作
作![]() 于點
于點![]() 將
將![]() 旋轉,得到
旋轉,得到![]() 為
為![]() 與
與![]() 的交點,
的交點,![]() 為
為![]() 與
與![]() 延長線的交點,現有以下結論:
延長線的交點,現有以下結論:
![]() ;
;
![]() 若
若![]() ;
;
![]() 若
若![]() ,則
,則![]() ;
;
![]() 若
若![]() 且
且![]() 時,
時,![]() .
.
其中正確的結論是_____________________(填寫所有正確結論的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
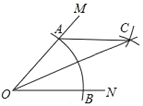
【題目】如圖,在∠MON中,以點O為圓心,任意長為半徑作弧,交射線OM于點A,交射線ON于點B,再分別以A、B為圓心,OA的長為半徑作弧,兩弧在∠MON的內部交于點C,作射線OC,若OA=5,AB=6,則點B到AC的距離為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
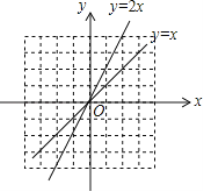
【題目】在平面直角坐標系xOy中,⊙C的半徑為r(r>1),P是圓內與圓心C不重合的點,⊙C的“完美點”的定義如下:若直線CP與⊙C交于點A,B,滿足|PA﹣PB|=2,則稱點P為⊙C的“完美點”,如圖為⊙C及其“完美點”P的示意圖.
(1)當⊙O的半徑為2時,
①在點M![]() ,N(0,1),T
,N(0,1),T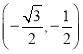 中,⊙O的“完美點”是 ;
中,⊙O的“完美點”是 ;
②若⊙O的“完美點”P在直線y=![]() x上,求PO的長及點P的坐標;
x上,求PO的長及點P的坐標;
(2)⊙C的圓心在直線y=![]() x+1上,半徑為2,若y軸上存在⊙C的“完美點”,求圓心C的縱坐標t的取值范圍.
x+1上,半徑為2,若y軸上存在⊙C的“完美點”,求圓心C的縱坐標t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
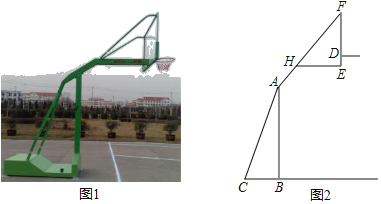
【題目】如圖1,2分別是某款籃球架的實物圖與示意圖,AB⊥BC于點B,底座BC=1.3米,底座BC與支架AC所成的角∠ACB=60°,點H在支架AF上,籃板底部支架EH∥BC.EF⊥EH于點E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求籃板底部支架HE與支架AF所成的∠FHE的度數.
(2)求籃板底部點E到地面的距離,(精確到0.01米)(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
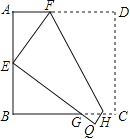
【題目】如圖,將邊長為6的正方形ABCD折疊,使點D落在AB邊的中點E處,折痕為FH,點C落在點Q處,EQ與BC交于點G,則△EBG的周長是 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在綠化某縣城與高速公路的連接路段中,需購買羅漢松、雪松兩種樹苗共400株,羅漢松樹苗每株60元,雪松樹苗每株70元.相關資料表明:羅漢松、雪松樹苗的成活率分別為70%,90%.
(1)若購買這兩種樹苗共用去26500元,則羅漢松、雪松樹苗各購買多少株?
(2)綠化工程來年一般都要將死樹補上新苗,現要使該兩種樹苗來年共補苗不多于80株,則羅漢松樹苗至多購買多少株?
(3)在(2)的條件下,應如何選購樹苗,才能使購買樹苗的費用最低?請求出最低費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,對角線AC,BD交于點O,且AC⊥BC,點E是BC延長線上一點, ![]() ,連接DE.
,連接DE.
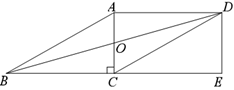
(1)求證:四邊形ACED為矩形;
(2)連接OE,如果BD=10,求OE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com