

| x | … | -7 | -6 | -4 | -3 | -2 | -1 | 0 | 1 | 3 | 4 | … |
| y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
分析 (1)當拋物線在x軸上方部分進滿足條件,可確定出對應的x的取值范圍;
(2)①由二次根式的意義可得到(x+1)(x+2)≥0,可轉化為(1);②利用描點法可畫出函數圖象;③結合圖象可得出答案.
解答 解:
(1)x2+3x+2>0的解集即拋物線在x軸上方部分對應的自變量的取值范圍,
∴x<-2或x>-1,
故答案為:<-2或x>-1;
(2)①由題意可得(x+1)(x+2)≥0,
由(1)可得x≤-2或x≥-1,
故答案為:x≤-2或x≥-1;
②如圖: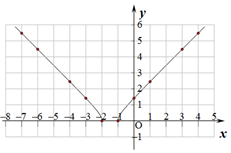
③由圖象可知關于直線x=-1.5對稱,
故答案為:關于直線x=-1.5對稱.
點評 本題主要考查二次函數的性質及函數與方程不等式的關系,利用數形結合是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3<h<5 | B. | 5<h<10 | C. | 10<h<15 | D. | 15<h<20 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2條 | B. | 3條 | C. | 4條 | D. | 無數條 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3a2-(2a-b+5c)=3a2-2a+b-5c | B. | 5x2+(-2x+y)-(3z-a)=5x2-2x+y-3z+a | ||
| C. | 2m2-3(m-1)=2m2-3m-1 | D. | -(2x-y)-(-x2+y2)=-2x+y+x2-y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com