【題目】已知a、b是一元二次方程x2+x﹣1＝0的兩根，則a+b＝_____．
科目：初中數學 來源： 題型：
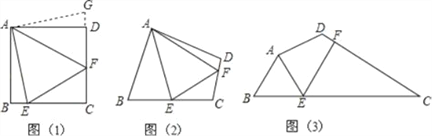
【題目】問題：如圖(1)，點E、F分別在正方形ABCD的邊BC、CD上，∠EAF=45°，試判斷BE、EF、FD之間的數量關系．
【發(fā)現證明】小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發(fā)現EF=BE+FD,請你利用圖（1）證明上述結論．
【類比引申】如圖(2)，四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足 關系時，仍有EF=BE+FD．
【探究應用】如圖(3)，在某公園的同一水平面上，四條通道圍成四邊形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分別有景點E、F，且AE⊥AD，DF=40（
﹣1）米，現要在E、F之間修一條筆直道路，求這條道路EF的長（結果取整數，參考數據： 
=1.41， 
=1.73）
查看答案和解析>>
科目：初中數學 來源： 題型：
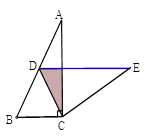
【題目】如圖，在Rt△ABC中，∠A=30°，BC=2，將△ABC繞點C按順時針方向旋轉n度后，得到△EDC，此時點D在AB邊上，斜邊DE交AC于點F，則n=_______; 圖中陰影部分的面積為____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，已知點P（2，1）與點Q（2，﹣1），下列描述正確是（ ）
A. 關于x軸對稱 B. 關于y軸對稱 C. 關于原點對稱 D. 都在y=2x的圖象上
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將等腰直角三角板放在正方形ABCD的頂點B處，且三角板中BE=EF．連AE，再作EG⊥AE且EG=AE．繞點B旋轉三角板，并保證線段FG與正方形的邊CD交于點H．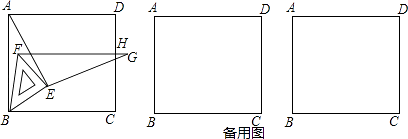
（1）求證：△ABE≌△GFE．
（2）當DH取得最小值時，求∠ABE的度數．
（3）當三角板有兩個頂點在邊BC上時，求 
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD的對角線相交于點O，AE平分∠BAD交BC于E，若∠CAE=15°，則∠AEO=（ ）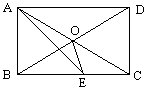
A.30°
B.25°
C.22.5°
D.20
查看答案和解析>>
科目：初中數學 來源： 題型：
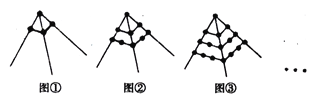
【題目】探索與推斷：
（1）有四個數，把其中每三個數相加，其和分別為22，24，27，20．求這四個數分別為多少？
（2）觀察下列圖形中的點的個數，若按其規(guī)律再畫下去：
①請你畫出第4個圖形，并指出第4個圖形中的點的個數；
②第n個圖形中所有點的個數是多少？（用含n的代數式表示）
③若圖形中共有1600個點，則該圖是第幾個圖形？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
