

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
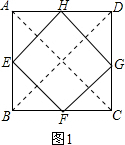 解:(1)如圖1.連接AC、BD.
解:(1)如圖1.連接AC、BD.| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
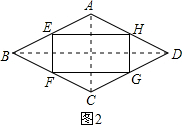 (2)如圖2.連接AC、BD.
(2)如圖2.連接AC、BD.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
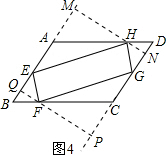 (4)S1=2S2.理由如下:
(4)S1=2S2.理由如下:| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
某班甲、乙、丙三位同學進行了一次用正方形紙片折疊探究相關數學問題的課題學習活動.
活動情境:
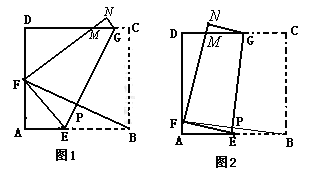
如圖2,將邊長為8cm的正方形紙片ABCD沿EG折疊(折痕EG分別與AB、DC交于點E、G),使點B落在AD邊上的點 F處,FN與DC交于點M處,連接BF與EG交于點P.
所得結論:
當點F與AD的中點重合時:(如圖1)甲、乙、丙三位同學各得到如下一個正確結論(或結果):
甲:△AEF的邊AE= cm,EF= cm;
乙:△FDM的周長為16 cm;
丙:EG=BF.
你的任務:
1.填充甲同學所得結果中的數據;
2. 寫出在乙同學所得結果的求解過程;
3.當點F在AD邊上除點A、D外的任何一處(如圖2)時:
① 試問乙同學的結果是否發生變化?請證明你的結論;
② 丙同學的結論還成立嗎?若不成立,請說明理由,若你認為成立,先證明EG=BF,再求出S(S為四邊形AEGD的面積)與x(AF=x)的函數關系式,并問當x為何值時,S最大?最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2012年江西省中等學校招生統一考試數學卷(一) 題型:解答題
某班甲、乙、丙三位同學進行了一次用正方形紙片折疊探究相關數學問題的課題學習活動.
活動情境:
如圖2,將邊長為8cm的正方形紙片ABCD沿EG折疊(折痕EG分別與AB、DC交于點E、G),使點B落在AD邊上的點 F處,FN與DC交于點M處,連接BF與EG交于點P.
所得結論:
當點F與AD的中點重合時:(如圖1)甲、乙、丙三位同學各得到如下一個正確結論(或結果):
甲:△AEF的邊AE= cm,EF= cm;
乙:△FDM的周長為16 cm;
丙:EG=BF.
你的任務:
【小題1】填充甲同學所得結果中的數據;
【小題2】 寫出在乙同學所得結果的求解過程;
【小題3】當點F在AD邊上除點A、D外的任何一處(如圖2)時:
① 試問乙同學的結果是否發生變化?請證明你的結論;
② 丙同學的結論還成立嗎?若不成立,請說明理由,若你認為成立,先證明EG=BF,再求出S(S為四邊形AEGD的面積)與x(AF=x)的函數關系式,并問當x為何值時,S最大?最大值是多少?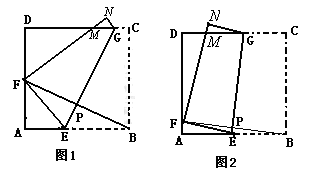
查看答案和解析>>
科目:初中數學 來源:2012年江西省等學校招生統一考試數學卷(一) 題型:解答題
某班甲、乙、丙三位同學進行了一次用正方形紙片折疊探究相關數學問題的課題學習活動.
活動情境:
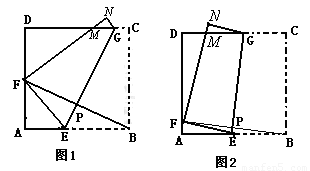
如圖2,將邊長為8cm的正方形紙片ABCD沿EG折疊(折痕EG分別與AB、DC交于點E、G),使點B落在AD邊上的點 F處,FN與DC交于點M處,連接BF與EG交于點P.
所得結論:
當點F與AD的中點重合時:(如圖1)甲、乙、丙三位同學各得到如下一個正確結論(或結果):
甲:△AEF的邊AE= cm,EF= cm;
乙:△FDM的周長為16 cm;
丙:EG=BF.
你的任務:
1.填充甲同學所得結果中的數據;
2. 寫出在乙同學所得結果的求解過程;
3.當點F在AD邊上除點A、D外的任何一處(如圖2)時:
① 試問乙同學的結果是否發生變化?請證明你的結論;
② 丙同學的結論還成立嗎?若不成立,請說明理由,若你認為成立,先證明EG=BF,再求出S(S為四邊形AEGD的面積)與x(AF=x)的函數關系式,并問當x為何值時,S最大?最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com