Question

如圖，在平面直角坐標系中，已知點A、B、C的坐標分別為（－1,0），（5,0），（0,2）
【小題1】求過A、B、C三點的拋物線解析式．
【小題2】若點P從Ａ點出發，沿x軸正方向以每秒1個單位長度的速度向B點移動，連接PC并延長到點E，使CE=PC，將線段PE繞點P順時針旋轉90°得到線段PF,連接FB．若點P運動的時間為ｔ秒，（0≤t≤6）設△PBF的面積為S．
①求S與ｔ的函數關系式．
②當ｔ是多少時，△PBF的面積最大，最大面積是多少？
【小題3】點P在移動的過程中，△PBF能否成為直角三角形？若能，直接寫出點F的坐標；若不能，請說明理由．

Answer 1

【小題1】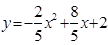
【小題2】①s=(t－2.5)²－6.25  ②S_最大=6
【小題3】能  , t=2或t= 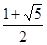時,△PFB是直角三角形     

解析

解： 設拋物線的解析式為

      把（0,2）代入解析式得                                       
，　
（2）過點F作FD⊥x軸于D

①當點P在原點左側時，BP=6－t,  OP=1－t       
在Rt△POC中，∠PCO+∠CPO=90°
∵∠FPD+∠CPO=90°
∴∠PCO=∠FPD
∵∠POC=∠FDP
∴△CPO∽△PFD                                      
∴ 
∵PF=PE=2PC
∴FD=2PO=2（1－t）                                         
∴S=                   
=t²－7t+6   (0≤t≤1)                        
=(t－2.5)²－6.25
∵1＞0
∴t≤2.5 時， s隨著t增大而減小
而0≤t≤1 ∴當t=0時S_最大=6
②當點P在原點右側時，OP=t－1，  BP=6－t
∴S△PBF=－t²+7t-6=－(t－3.5)² +6.25  (1≤t≤6)
∵－1＞0
∴t＝3.5 時， S_最大=6.25＞6
∴當t=3.5時，△PFB面積最大，最大面積為6.25.
（3）能                                                  
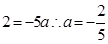
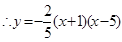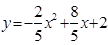
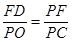
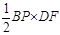
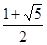t=2或t= 時,△PFB是直角三角形