
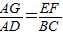 ,求出即可;
,求出即可;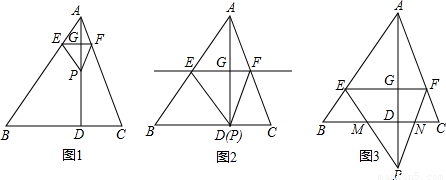 解:(1)∵EF∥BC,
解:(1)∵EF∥BC,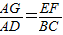 ,
,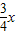 ;
; x,
x, ×x×
×x× x=
x= x2,
x2,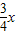 ,AD=3,
,AD=3,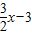
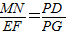 ,
,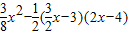 =
=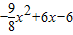 ,
,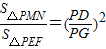 ,
,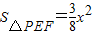 ,
,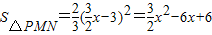 ,
,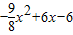 .
.

 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
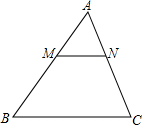 BCNM內的點A′,△A′MN與四邊形BCNM重疊部分的面積為y.
BCNM內的點A′,△A′MN與四邊形BCNM重疊部分的面積為y.查看答案和解析>>
科目:初中數學 來源: 題型:
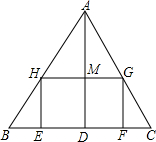 一個長HG是寬HE的2倍的矩形EFGH.使它的一邊EF在BC上,頂點G,H分別在AC,AB上.AD與HG的交點為M.
一個長HG是寬HE的2倍的矩形EFGH.使它的一邊EF在BC上,頂點G,H分別在AC,AB上.AD與HG的交點為M.| AM |
| AD |
| HG |
| BC |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com