
【題目】當圖形具有鄰邊相等的特征時,我們可以把圖形的一部分繞著公共端點旋轉,這樣將分散的條件集中起來,從而達到解決問題的目的
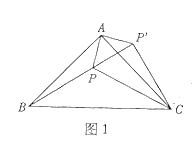
![]() 如圖1,等腰直角三角形
如圖1,等腰直角三角形![]() 內有一點
內有一點![]() 連接
連接![]() 為探究
為探究![]() 三條線段間的數量關系,我們可以將
三條線段間的數量關系,我們可以將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() 連接
連接![]() 則
則![]() ___ ____
___ ____![]() 是_ 三角形,
是_ 三角形,![]() 三條線段的數量關系是_ ;
三條線段的數量關系是_ ;
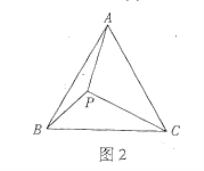
![]() 如圖2,等邊三角形
如圖2,等邊三角形![]() 內一點P,連接
內一點P,連接![]() 請借助第一問的方法探究
請借助第一問的方法探究![]() 三條線段間的數量關系.
三條線段間的數量關系.
![]() 如圖3 ,在四邊形
如圖3 ,在四邊形![]() 中,
中,![]() 點
點![]() 在四邊形內部,且
在四邊形內部,且![]()
![]() 請直接寫出
請直接寫出![]() 的長.
的長.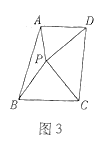
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 上,
上,![]() ,連結
,連結![]() ,點
,點![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 的中點.
的中點.

(1)觀察猜想圖1中,線段![]() 與
與![]() 的數量關系是_______,位置關系是_______;
的數量關系是_______,位置關系是_______;
(2)探究證明把![]() 繞點
繞點![]() 逆時針方向旋轉到圖2的位置,連結
逆時針方向旋轉到圖2的位置,連結![]() 、
、![]() 、
、![]() ,判斷
,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)拓展延伸把![]() 繞點
繞點![]() 在平面內自由旋轉,若
在平面內自由旋轉,若![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016湖北省黃岡市)如圖,已知點A(1,a)是反比例函數![]() 的圖象上一點,直線
的圖象上一點,直線![]() 與反比例函數
與反比例函數![]() 的圖象在第四象限的交點為點B.
的圖象在第四象限的交點為點B.
(1)求直線AB的解析式;
(2)動點P(x,0)在x軸的正半軸上運動,當線段PA與線段PB之差達到最大時,求點P的坐標.
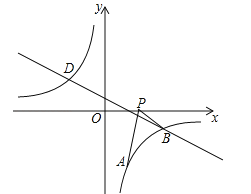
【答案】(1)y=x﹣4;(2)P(4,0).
【解析】試題分析:(1)先把A(1,a)代入反比例函數解析式求出a得到A點坐標,再解方程組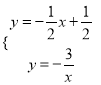 ,得B點坐標,然后利用待定系數法求AB的解析式;
,得B點坐標,然后利用待定系數法求AB的解析式;
(2)直線AB交x軸于點Q,如圖,利用x軸上點的坐標特征得到Q點坐標,則PA﹣PB≤AB(當P、A、B共線時取等號),于是可判斷當P點運動到Q點時,線段PA與線段PB之差達到最大,從而得到P點坐標.
試題解析:(1)把A(1,a)代入![]() 得a=﹣3,則A(1,﹣3),解方程組:
得a=﹣3,則A(1,﹣3),解方程組: 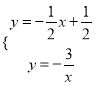 ,得:
,得: ![]() 或
或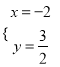 ,則B(3,﹣1),設直線AB的解析式為y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:
,則B(3,﹣1),設直線AB的解析式為y=kx+b,把A(1,﹣3),B(3,﹣1)代入得: ![]() ,解得:
,解得: ![]() ,所以直線AB的解析式為y=x﹣4;
,所以直線AB的解析式為y=x﹣4;
(2)直線AB交x軸于點Q,如圖,當y=0時,x﹣4=0,解得x=4,則Q(4,0),因為PA﹣PB≤AB(當P、A、B共線時取等號),所以當P點運動到Q點時,線段PA與線段PB之差達到最大,此時P點坐標為(4,0).
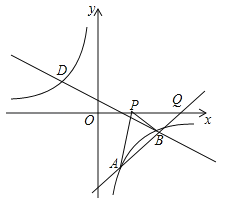
考點:反比例函數與一次函數的交點問題.
【題型】解答題
【結束】
22
【題目】成都三圣鄉花卉基地出售兩種盆栽花卉:太陽花6元/盆,繡球花10元/盆.若一次購買的繡球花超過20盆時,超過20盆部分的繡球花價格打8折.
(1)若小張家花臺綠化需用60盆兩種盆栽花卉,小張爸爸給他460元錢去購買,問兩種花卉各買了多少盆?
(2)分別寫出兩種花卉的付款金額y(元)關于購買量x(盆)的函數解析式;
(3)為了美化環境,花園小區計劃到該基地購買這兩種花卉共90盆,其中太陽花數量不超過繡球花數量的一半.兩種花卉各買多少盆時,總費用最少,最少費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點![]() 是以
是以![]() 為直徑的半圓
為直徑的半圓![]() 上任意一點(不與點
上任意一點(不與點![]() 重合),連接
重合),連接![]() 并延長至點
并延長至點![]() 使
使![]() 連接
連接![]() 交半圓
交半圓![]() 于點
于點![]() 過點
過點![]() 作
作![]() 于點
于點![]() .
.

![]() 求證:
求證:![]() .
.
![]() 如圖2,連接
如圖2,連接![]() .
.
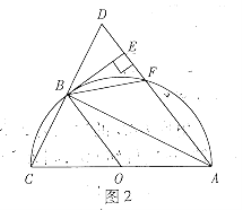
①當![]()
![]() 時,四邊形
時,四邊形![]() 是菱形;
是菱形;
②當![]()
![]() 時,四邊形
時,四邊形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某社區為了加強社區居民對新型冠狀病毒肺炎防護知識的了解,通過微信群宣傳新型冠狀病毒肺炎的防護知識,并鼓勵社區居民在線參與作答《2020年新型冠狀病毒防治全國統一考試(全國卷)》試卷(滿分100分),社區管理員隨機從有400人的某小區抽取40名人員的答卷成績,并對他們的成績(單位:分)統計如下:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
根據數據繪制了如下的表格和統計圖:
等級 | 成績( | 頻率 | 頻率 |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
合計 | 40 | 1 | |
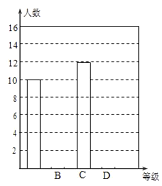
根據上面提供的信息,回答下列問題:
(1)統計表中的![]() ,
,![]() ;
;
(2)請補全條形統計圖;
(3)根據抽樣調查結果,請估計該小區答題成績為“![]() 級”的有多少人?
級”的有多少人?
(4)該社區有2名男管理員和2名女管理員,現從中隨機挑選2名管理員參加“社區防控”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在一條長為600m的筆直道路上均勻地跑步,速度分別為![]() 和
和![]() ,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
A.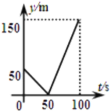 B.
B. C.
C.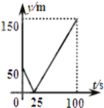 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 中點,點
中點,點![]() 在
在![]() 延長線上,
延長線上,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() .
.
(1)若![]() ,求
,求![]() 的度數;
的度數;
(2)求證:![]() ;
;
(3)設![]() 交
交![]() 于點
于點![]() .
.
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②連結![]() ,分別記
,分別記![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() ,
,![]() ,
,![]() ,當
,當![]() 時,
時,![]() .(直接寫出答案)
.(直接寫出答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com