
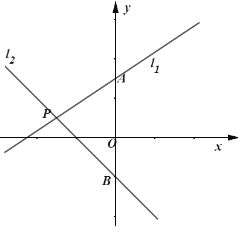
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() :
:![]() 交
交![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 點
點![]() .
.
(1)求直線![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)過動點![]() 作
作![]() 軸的垂線與直線
軸的垂線與直線![]() 、
、![]() 分別交于
分別交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
①求![]() 的取值范圍;
的取值范圍;
②若![]() ,直接寫出
,直接寫出![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() 且
且![]() ;②
;② ![]() 或
或![]()
【解析】
(1)利用![]() 求出
求出![]() 點坐標為
點坐標為![]() ,再設(shè)直線
,再設(shè)直線![]() 的函數(shù)解析式為y=kx+b,將點A、P的坐標代入解答;
的函數(shù)解析式為y=kx+b,將點A、P的坐標代入解答;
(2)①由已知可得:![]() 、
、![]() 兩點的坐標分別為:
兩點的坐標分別為:![]() ,
,![]() ,分兩種情況:當點
,分兩種情況:當點![]() 在點
在點![]() 右側(cè)時,點
右側(cè)時,點![]() 在點
在點![]() 的上方,求出
的上方,求出![]() 解得
解得![]() ,當點
,當點![]() 在點
在點![]() 左側(cè)時,點
左側(cè)時,點![]() 在點
在點![]() 的下方,求得
的下方,求得![]() 解得
解得![]() ,由此動點a的取值范圍;
,由此動點a的取值范圍;
②設(shè)![]() ,連接AN1,作N1D⊥y軸于D,PC⊥y軸于C,根據(jù)
,連接AN1,作N1D⊥y軸于D,PC⊥y軸于C,根據(jù)![]() ,求出OD=1+3=4,由此得到點N1的橫坐標是-6,即a=-6;設(shè)
,求出OD=1+3=4,由此得到點N1的橫坐標是-6,即a=-6;設(shè)![]() ,,連接AN2,作N2D⊥y軸于D,PC⊥y軸于C,根據(jù)
,,連接AN2,作N2D⊥y軸于D,PC⊥y軸于C,根據(jù)![]() ,求出CD=
,求出CD=![]() CB=1,得到點N2的縱坐標是0,由此解得x=-2,得到a=-2.
CB=1,得到點N2的縱坐標是0,由此解得x=-2,得到a=-2.
(1)將點P的坐標代入![]() 中,得t=3-2=1,
中,得t=3-2=1,
∴![]() 點坐標為
點坐標為![]() ,
,
設(shè)直線![]() 的函數(shù)解析式為y=kx+b,將點A、P的坐標代入,得
的函數(shù)解析式為y=kx+b,將點A、P的坐標代入,得
![]() ,解得
,解得![]() ,
,
∴直線![]() 的函數(shù)解析式為
的函數(shù)解析式為![]() ;
;
(2)①由已知可得:![]() 、
、![]() 兩點的坐標分別為:
兩點的坐標分別為:![]() ,
,![]() ,
,
當點![]() 在點
在點![]() 右側(cè)時,點
右側(cè)時,點![]() 在點
在點![]() 的上方,
的上方,
∴![]() 解得
解得![]() ,
,
當點![]() 在點
在點![]() 左側(cè)時,點
左側(cè)時,點![]() 在點
在點![]() 的下方,
的下方,
∴![]() 解得
解得![]() ,
,
綜上![]() 的取值范圍是:
的取值范圍是:![]() 且
且![]() (注:沒有
(注:沒有![]() 不扣分);
不扣分);
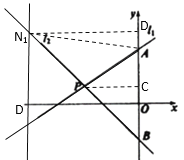
②設(shè)![]() ,連接AN1,作N1D⊥y軸于D,PC⊥y軸于C,
,連接AN1,作N1D⊥y軸于D,PC⊥y軸于C,
∵![]() ,
,
∴N1P=PB,
∵B(0,-2),
∴CD=CB=1-(-2)=3,
∴OD=1+3=4,
將y=4代入y=-x-2中得-x-2=4,
解得x=-6,
∴點N1的橫坐標是-6,即a=-6;
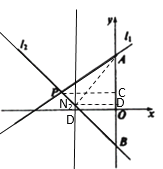
設(shè)![]() ,連接AN2,作N2D⊥y軸于D,PC⊥y軸于C,
,連接AN2,作N2D⊥y軸于D,PC⊥y軸于C,
∵![]() ,
,
∴PN2=![]() PB,
PB,
∴CD=![]() CB=1,
CB=1,
∴點N2的縱坐標是0,
將y=0代入y=-x-2中,得x=-2,
∴a=-2,
綜上,![]() 或
或![]() .
.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數(shù)學 來源: 題型:
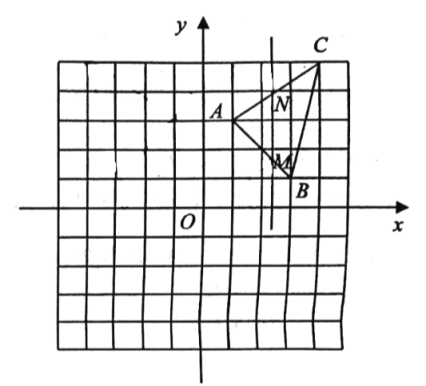
【題目】如圖,在平面直角坐標系中,點![]() ,點
,點![]() ,點
,點![]() .
.
(1)畫出![]() 關(guān)于
關(guān)于![]() 軸的對稱圖形
軸的對稱圖形![]() ,并寫出點
,并寫出點![]() 的對稱點
的對稱點![]() 的坐標;
的坐標;
(2)若點![]() 在
在![]() 軸上,連接
軸上,連接![]() 、
、![]() ,則
,則![]() 的最小值是 ;
的最小值是 ;
(3)若直線![]() 軸,與線段
軸,與線段![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() (點
(點![]() 不與點
不與點![]() 重合),若將
重合),若將![]() 沿直線
沿直線![]() 翻折,點
翻折,點![]() 的對稱點為點
的對稱點為點![]() ,當點
,當點![]() 落在
落在![]() 的內(nèi)部(包含邊界)時,點
的內(nèi)部(包含邊界)時,點 的橫坐標
的橫坐標![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知點P(2,﹣3)在拋物線L:y=ax2﹣2ax+a+k(a,k均為常數(shù)且a≠0)上,L交y軸于點C,連接CP.
(1)用a表示k,并求L的對稱軸;
(2)當L經(jīng)過點(4,﹣7)時,求此時L的表達式及其頂點坐標;
(3)橫,縱坐標都是整數(shù)的點叫做整點.如圖,當a<0時,若L在點C,P之間的部分與線段CP所圍成的區(qū)域內(nèi)(不含邊界)恰有5個整點,求a的取值范圍;
(4)點M(x1,y1),N(x2,y2)是L上的兩點,若t≤x1≤t+1,當x2≥3時,均有y1≥y2,直接寫出t的取值范圍.
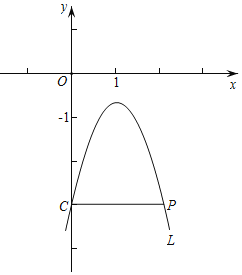
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
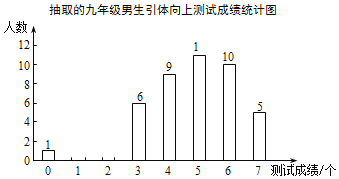
【題目】某中學九年級男生共250人,現(xiàn)隨機抽取了部分九年級男生進行引體向上測試,相關(guān)數(shù)據(jù)的統(tǒng)計圖如下.設(shè)學生引體向上測試成績?yōu)?/span>x(單位:個).學校規(guī)定:當0≤x<2時成績等級為不及格,當2≤x<4時成績等級為及格,當4≤x<6時成績等級為良好,當x≥6時成績等級為優(yōu)秀.樣本中引體向上成績優(yōu)秀的人數(shù)占30%,成績?yōu)?/span>1個和2個的人數(shù)相同.
(1)補全統(tǒng)計圖;
(2)估計全校九年級男生引體向上測試不及格的人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
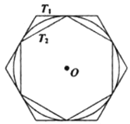
【題目】如圖,有一個圓![]() 和兩個正六邊形
和兩個正六邊形![]() ,
,![]() .
.![]() 的6個頂點都在圓周上,
的6個頂點都在圓周上,![]() 的6條邊都和圓
的6條邊都和圓![]() 相切(我們稱
相切(我們稱![]() ,
,![]() 分別為圓
分別為圓![]() 的外切正六邊形和內(nèi)接正六邊形),若設(shè)
的外切正六邊形和內(nèi)接正六邊形),若設(shè)![]() ,
,![]() 的周長分別為
的周長分別為![]() ,
,![]() ,圓
,圓![]() 的半徑為
的半徑為![]() ,則
,則![]() ___;
___;![]() ____;正六邊形
____;正六邊形![]() ,
,![]() 的面積比
的面積比![]() 的值是____.
的值是____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
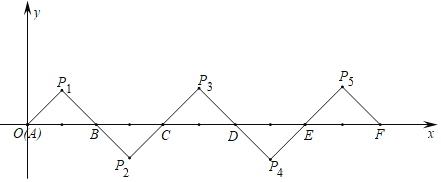
【題目】如圖所示,在平面直角坐標系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 繞點B順時針旋轉(zhuǎn)
繞點B順時針旋轉(zhuǎn)![]() ,得到
,得到![]() ,把
,把![]() 繞點C順時針旋轉(zhuǎn)
繞點C順時針旋轉(zhuǎn)![]() ,得到
,得到![]() ,依此類推,得到的等腰直角三角形的直角頂點
,依此類推,得到的等腰直角三角形的直角頂點![]() 的坐標為__________.
的坐標為__________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經(jīng)過
經(jīng)過![]() 兩點,與
兩點,與![]() 軸的另一個交點為
軸的另一個交點為![]() ,點
,點![]() 是第一象限拋物線上的點,連結(jié)
是第一象限拋物線上的點,連結(jié)![]() 交直線
交直線![]() 于點
于點![]() ,設(shè)點
,設(shè)點![]() 的橫坐為
的橫坐為![]() ,
,![]() 與
與![]() 的比值為
的比值為![]() .
.
(1)![]() __________;
__________;
(2)當![]() 取最大值時,
取最大值時,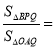 __________.
__________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
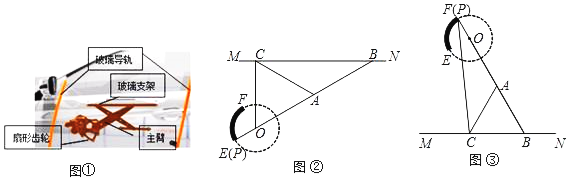
【題目】我們常見的汽車玻璃升降器如圖①所示,圖②和圖③是升降器的示意圖,其原理可以看作是主臂PB繞固定的點O旋轉(zhuǎn),當端點P在固定的扇形齒輪![]() 上運動時,通過叉臂式結(jié)構(gòu)(點B可在MN上滑動)的玻璃支架MN帶動玻璃沿導軌作上下運動而達到玻璃升降目的.點O和點P,A,B在同一直線上.當點P與點E重合時,窗戶完全閉合(圖②),此時∠ABC=30°;當點P與點F重合時,窗戶完全打開(圖③).已知
上運動時,通過叉臂式結(jié)構(gòu)(點B可在MN上滑動)的玻璃支架MN帶動玻璃沿導軌作上下運動而達到玻璃升降目的.點O和點P,A,B在同一直線上.當點P與點E重合時,窗戶完全閉合(圖②),此時∠ABC=30°;當點P與點F重合時,窗戶完全打開(圖③).已知![]() 的半徑OP=5cm,
的半徑OP=5cm,![]() =
=![]() cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.
(1)當窗戶完全閉合時,OC=_____cm.
(2)當窗戶完全打開時,PC=_____cm.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】學校開展“書香校園”活動以來,受到同學們的廣泛關(guān)注,學校為了解全校學生課外閱讀的情況,隨機調(diào)查了部分學生在一周內(nèi)借閱圖書的次數(shù),并制成如圖不完整的統(tǒng)計表
學生借閱圖書的次數(shù)
借閱圖書的次數(shù) | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人數(shù) | 7 | 13 | a | 10 | 3 |
學生借閱圖書的次數(shù)統(tǒng)計表

請你根據(jù)統(tǒng)計圖表的信息,解答下列問題:
(1)a= ;b=
(2)該調(diào)查統(tǒng)計數(shù)據(jù)的中位數(shù)是__________次
(3)扇形統(tǒng)計圖中,“3次”所對應的扇形圓心角度數(shù)是______________;
(4)若該校共有2000名學生,根據(jù)調(diào)查結(jié)果,估計該校學生在一周內(nèi)借閱圖書“4次以上”的人數(shù)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com