
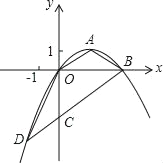
【題目】如圖,頂點為A(![]() ,1)的拋物線經過坐標原點O,與x軸交于點B.
,1)的拋物線經過坐標原點O,與x軸交于點B.
(1)求拋物線對應的二次函數的表達式;
(2)過B作OA的平行線交y軸于點C,交拋物線于點D,求證:△OCD≌△OAB;
(3)在x軸上找一點P,使得△PCD的周長最小,求出P點的坐標.
【答案】(1)y=﹣![]() x2+
x2+![]() x;(2)見解析;(3)點P的坐標為(﹣
x;(2)見解析;(3)點P的坐標為(﹣![]() ,0)
,0)
【解析】試題分析:(1)用待定系數法求出拋物線解析式,(2)先求出直線OA對應的一次函數的表達式為y=![]() x.再求出直線BD的表達式為y=
x.再求出直線BD的表達式為y=![]() x﹣2.最后求出交點坐標C,D即可;
x﹣2.最后求出交點坐標C,D即可;
(3)先判斷出C'D與x軸的交點即為點P,它使得△PCD的周長最小.作輔助線判斷出△C'PO∽△C'DQ即可.
試題解析:解:(1)∵拋物線頂點為A(![]() ,1),設拋物線解析式為y=a(x﹣
,1),設拋物線解析式為y=a(x﹣![]() )2+1,將原點坐標(0,0)在拋物線上,∴0=a(
)2+1,將原點坐標(0,0)在拋物線上,∴0=a(![]() )2+1
)2+1
∴a=﹣![]() ,∴拋物線的表達式為:y=﹣
,∴拋物線的表達式為:y=﹣![]() x2+
x2+![]() x.
x.
(2)令y=0,得 0=﹣![]() x2+
x2+![]() x,∴x=0(舍),或x=2
x,∴x=0(舍),或x=2![]()
∴B點坐標為:(2![]() ,0),設直線OA的表達式為y=kx.∵A(
,0),設直線OA的表達式為y=kx.∵A(![]() ,1)在直線OA上,∴
,1)在直線OA上,∴![]() k=1,∴k=
k=1,∴k=![]() ,∴直線OA對應的一次函數的表達式為y=
,∴直線OA對應的一次函數的表達式為y=![]() x.
x.
∵BD∥AO,設直線BD對應的一次函數的表達式為y=![]() x+b.∵B(2
x+b.∵B(2![]() ,0)在直線BD上,∴0=
,0)在直線BD上,∴0=![]() ×2
×2![]() +b,∴b=﹣2,∴直線BD的表達式為y=
+b,∴b=﹣2,∴直線BD的表達式為y=![]() x﹣2.
x﹣2.
由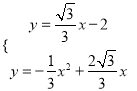
得交點D的坐標為(﹣![]() ,﹣3),令x=0得,y=﹣2,∴C點的坐標為(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2
,﹣3),令x=0得,y=﹣2,∴C點的坐標為(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2![]() =OD.
=OD.
在△OAB與△OCD中, 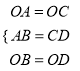 ,∴△OAB≌△OCD.
,∴△OAB≌△OCD.
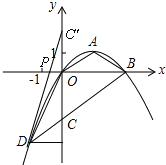
(3)點C關于x軸的對稱點C'的坐標為(0,2),∴C'D與x軸的交點即為點P,它使得△PCD的周長最小.
過點D作DQ⊥y,垂足為Q,∴PO∥DQ,∴△C'PO∽△C'DQ,∴![]() ,∴
,∴![]() ,∴PO=
,∴PO=![]() ,∴點P的坐標為(﹣
,∴點P的坐標為(﹣![]() ,0).
,0).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
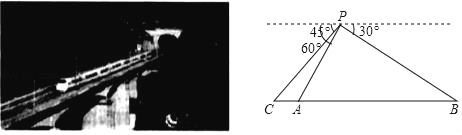
【題目】宜萬鐵路線上,一列列和諧號動車象一條條巨龍穿梭于恩施崇山峻嶺,大多地段橋梁與隧道交替相連如圖,勘測隊員在山頂P處測得山腳下隧道入口A點處的俯角為60°,隧道出口B點處的俯角為30°,一列動車以180km/h的速度自西向東行駛,當車頭抵達入口A點處時,車尾C點處的俯角是45°,整個車身全部進入隧洞恰好用了4s鐘時間,求車身完全在隧道中運行的時間(結果精確到1秒,參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732 ).
≈1.732 ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數y=mx2-(2m+1)x+m-5的圖象與x軸有兩個公共點.
(![]() )求m的取值范圍;
)求m的取值范圍;
(![]() )若m取滿足條件的最小的整數,
)若m取滿足條件的最小的整數,
①寫出這個二次函數的表達式;
②當n≤x≤1時,函數值y的取值范圍是-6≤y≤4-n,求n的值;
③將此二次函數圖象平移,使平移后的圖象經過原點O.設平移后的圖象對應的函數表達式為y=a(x-h)2 +k,當x<2時,y隨x的增大而減小,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
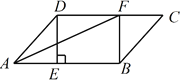
【題目】如圖,在平行四邊形![]() 中,過點
中,過點![]() 作
作![]() 于點
于點![]() ,點
,點![]() 在邊
在邊![]() 上,
上,![]() ,連接
,連接![]() ,
,![]() .
.
(1)求證:四邊形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小李某天下午運營全是在東西走向的人民大道上進行的,如果規定向東為正,向西為負,他這天下午行駛里程如下:(單位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他將最后一名乘客送到目的地時,距下午出車地點是多少千米?
(2)若汽車耗油量為![]() 升∕千米,這天下午共耗油多少升
升∕千米,這天下午共耗油多少升
查看答案和解析>>
科目:初中數學 來源: 題型:
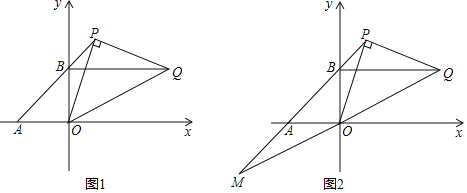
【題目】已知:如圖,直線AB交兩坐標軸于A(a,0)、B(0,b)兩點,且a,b滿足等式:![]() +(b﹣4)2=0,點P為直線AB上第一象限內的一動點,過P作OP的垂線且與過B點且平行于x軸的直線相交于點Q,
+(b﹣4)2=0,點P為直線AB上第一象限內的一動點,過P作OP的垂線且與過B點且平行于x軸的直線相交于點Q,
(1)求A,B兩點的坐標;
(2)當P點在直線AB上的第一象限內運動時,![]() AP﹣BQ的值變不變?如果不變,請求出這個定值;若變化請說明理由.
AP﹣BQ的值變不變?如果不變,請求出這個定值;若變化請說明理由.
(3)延長QO與直線AB交于點M.請判斷出線段AP,BM,PM三條線段構成三角形的形狀,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD的邊長為1,點P為正方形內一動點,若點M在AB上,且滿足△PBC∽△PAM,延長BP交AD于點N,連結CM.

(1)如圖一,若點M在線段AB上,求證:AP⊥BN;AM=AN;
(2)①如圖二,在點P運動過程中,滿足△PBC∽△PAM的點M在AB的延長線上時,AP⊥BN和AM=AN是否成立?
②是否存在滿足條件的點P,使得PC=![]() ?(不需說明理由).
?(不需說明理由).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學舉行“中國夢校園好聲音”歌手大賽,高、初中部根據初賽成績,各選出5名選手組成初中代表隊和高中代表隊參加學校決賽。兩個隊各選出的5名選手的決賽成績如圖所示.
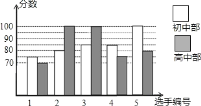
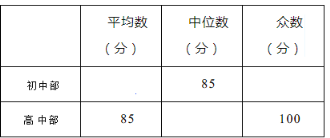
(1)根據圖示填寫下表;
(2)結合兩隊成績的平均數和中位數,分析哪個隊的決賽成績較好;
(3)計算兩隊決賽成績的方差并判斷哪一個代表隊選手成績較為穩定.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com