
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點.直線
為坐標原點.直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,
,![]() ,垂足為
,垂足為![]() ,交
,交![]() 軸負半軸于點
軸負半軸于點![]() ,且點
,且點![]() 坐標為
坐標為![]() .
.
(1)求直線![]() 的解析式;
的解析式;
(2)點![]() 為直線
為直線![]() 右側第一象限內一點,連接
右側第一象限內一點,連接![]() 、
、![]() ,將線段
,將線段![]() 繞點
繞點![]() 順時針旋轉90°,得到線段
順時針旋轉90°,得到線段![]() ,點
,點![]() 落在點
落在點![]() 處,設點
處,設點![]() 的坐標為
的坐標為![]() ,求點
,求點![]() 的坐標(用含
的坐標(用含![]() 的式子表示);
的式子表示);
(3)在(2)的條件下,過點![]() 作
作![]() 垂直于
垂直于![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,點
,點![]() 為
為![]() 延長線上一點,連接
延長線上一點,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,求點
,求點![]() 的坐標.
的坐標.
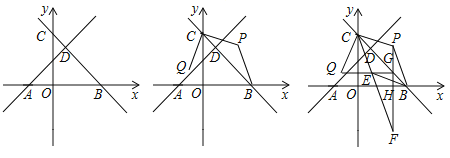
【答案】(1)y=x+2;;(2)Q(-![]() m2+m,4-m);(3)P(
m2+m,4-m);(3)P(![]() ,
,![]() ).
).
【解析】
(1)由已知可得∠DAO=45°,進而得到AD直線的k=1,將點A(-2,0)代入即可;
(2)過點P作x軸、y軸垂線,相交于點M,過點Q作y軸垂線,交于點N,由已知條件可證明△CQN≌△DMP(AAS),所以有QN=MP,CM=CN,即可求Q點坐標;
(3)由題意可求G(m,4-m),因此GQ與y軸垂直,由QG=GF,可求F(m,4-m-![]() m2),求出CF所在直線解析式為y=-(1+
m2),求出CF所在直線解析式為y=-(1+![]() m)x+4,確定點E(
m)x+4,確定點E(![]() ,4-m);過點E作ET垂直x軸,過點G作GS垂直PH,交PB于點S,可證明△ETB≌△HBP(HL),由平行的性質和等腰直角三角形的性質可知∠EGB=∠PGB=90°+45°=135°,得到△EGB≌△PGB(AAS),故有EG=PG,將點的坐標代入有m-
,4-m);過點E作ET垂直x軸,過點G作GS垂直PH,交PB于點S,可證明△ETB≌△HBP(HL),由平行的性質和等腰直角三角形的性質可知∠EGB=∠PGB=90°+45°=135°,得到△EGB≌△PGB(AAS),故有EG=PG,將點的坐標代入有m-![]() =-
=-![]() m2+m+4-(4-m),求出m即可.
m2+m+4-(4-m),求出m即可.
解:(1)由題意可知B(4,0),C(0,4),
∴CO=BO,
∴∠CBO=45°,
∵AD⊥BC,
∴∠DAO=45°,
∵A(-2,0),
∴AD的直線解析式為y=x+2;
(2)如圖,過點P作x軸、y軸垂線,相交于點M,過點Q作y軸垂線,交于點N,

∵∠PCQ=90°,∠MCN=90°,
∴∠MCP=∠NCQ,
∵CP=CQ,∠CNQ=∠CMP=90°,
∴△CQN≌△DMP(AAS),
∴QN=MP,CM=CN
∵P的坐標為(m,-![]() m2+m+4),
m2+m+4),
∴CM=m,MP=4-(-![]() m2+m+4)=
m2+m+4)=![]() m2-m,
m2-m,
∴Q(-![]() m2+m,4-m);
m2+m,4-m);
(3)如圖,

∵PH垂直于x軸,
∴G點橫坐標為m,
∵G點在直線BC上,
∴G(m,4-m),
∵QG=GF,
∴![]() m2=4-m-yF,
m2=4-m-yF,
∴F(m,4-m-![]() m2)
m2)
∴CF所在直線解析式為y=-(1+![]() m)x+4,
m)x+4,
∴E(![]() ,4-m),
,4-m),
過點E作ET垂直x軸,過點G作GS垂直PH,交PB于點S,
∴ET=4-m,HB=4-m,
∴ET=HB,
∵BE=BP,
∴△ETB≌△HBP(HL),
∴∠EBT=∠BPH,
∵QG∥OB,
∴∠EBT=∠GEB,
∴∠GEB=∠BPG,
∠EGB=∠PGB=90°+45°=135°,
∴△EGB≌△PGB(AAS),
∴EG=PG,
∴m-![]() =-
=-![]() m2+m+4-(4-m),
m2+m+4-(4-m),
∴m=±![]() ,
,
∵P為直線BC右側第一象限內一點,
∴m=![]() ,
,
∴P(![]() ,
,![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,MN//EF, 點C 為兩直線之間一點,若∠CAM 的平分線與∠CBF 的平分線所在的直線相交于點 D ,則∠ACB與 ∠ADB 之間的數量關系是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=﹣x+2的圖象與反比例函數y2= ![]() 的圖象相交于A,B兩點,點B的坐標為(2m,﹣m).
的圖象相交于A,B兩點,點B的坐標為(2m,﹣m).
(1)求出m值并確定反比例函數的表達式;
(2)請直接寫出當x<m時,y2的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=1,與x軸的一個交點坐標為(﹣1,0),其部分圖象如圖所示,下列結論:
①4ac<b2;
②方程ax2+bx+c=0的兩個根是x1=﹣1,x2=3;
③3a+c>0;
④當y>0時,x的取值范圍是﹣1≤x<3;
⑤當x<0時,y隨x增大而增大;
其中結論正確有 . 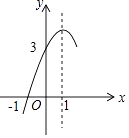
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料解決問題:
材料:古希臘著名數學家 畢達哥拉斯發現把數1,3,6,10,15,21…這些數量的(石子),都可以排成三角形,則稱像這樣的數為三角形數.
把數 1,3,6,10,15,21…換一種方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
從上面的排列方式看,把1,3,6,10,15,…叫做三角形數“名副其實”.
(1)設第一個三角形數為a1=1,第二個三角形數為a2=3,第三個三角形數為a3=6,請直接寫出第n個三角形數為an的表達式(其中n為正整數).
(2)根據(1)的結論判斷66是三角形數嗎?若是請說出66是第幾個三角形數?若不是請說明理由.
(3)根據(1)的結論判斷所有三角形數的倒數之和T與2的大小關系并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星光櫥具店購進電飯煲和電壓鍋兩種電器進行銷售,其進價與售價如表:
進價(元/臺) | 售價(元/臺) | |
電飯煲 | 200 | 250 |
電壓鍋 | 160 | 200 |
(1)一季度,櫥具店購進這兩種電器共30臺,用去了5600元,并且全部售完,問櫥具店在該買賣中賺了多少錢?
(2)為了滿足市場需求,二季度櫥具店決定用不超過9000元的資金采購電飯煲和電壓鍋共50臺,且電飯煲的數量不少于電壓鍋的![]() ,問櫥具店有哪幾種進貨方案?并說明理由;
,問櫥具店有哪幾種進貨方案?并說明理由;
(3)在(2)的條件下,請你通過計算判斷,哪種進貨方案櫥具店賺錢最多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一點,
上一點,![]() 于點
于點![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 于點
于點![]() ,與
,與![]() 交于點
交于點![]() ,若
,若![]() ,
,![]() 平分
平分![]() ,連結
,連結![]() ,
,![]() .
.

(1)求證:![]() ;
;
(2)求證:![]() .
.
(3)若![]() ,判定四邊形
,判定四邊形![]() 是否為菱形,并說明理由.
是否為菱形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖1,在平面直角坐標系中,點A,B,E分別是x軸和y軸上的任意點. BD是∠ABE的平分線,BD的反向延長線與∠OAB的平分線交于點C.
探究: (1)求∠C的度數.
發現: (2)當點A,點B分別在x軸和y軸的正半軸上移動時,∠C的大小是否發生變化?若不變,請直接寫出結論;若發生變化,請求出∠C的變化范圍.
應用:(3)如圖2在五邊形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延長線與∠EDC外角的平分線相交于點P,求∠P的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條東西走向河的一側有一村莊C,河邊原有兩個取水點A,B,其中AB=AC,由于某種原因,由C到A的路現在已經不通,某村為方便村民取水決定在河邊新建一個取水點H(A、H、B在一條直線上),并新修一條路CH,測得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)問CH是否為從村莊C到河邊的最近路?(即問:CH與AB是否垂直?)請通過計算加以說明;
(2)求原來的路線AC的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com