
【題目】閱讀材料:若拋物線![]() 的頂點
的頂點![]() 在拋物線
在拋物線![]() 上,拋物線
上,拋物線![]() 的頂點
的頂點![]() 也在拋物線
也在拋物線![]() 上(點
上(點![]() 與點
與點![]() 不重合),我們稱這樣的兩條拋物線
不重合),我們稱這樣的兩條拋物線![]() 、
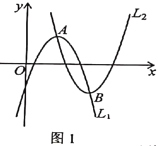
、![]() 互為“友好”拋物線,如圖1.
互為“友好”拋物線,如圖1.
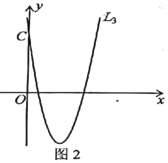
解決問題:如圖2,已知物線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
(1)若點![]() 與點
與點![]() 關于拋物線
關于拋物線![]() 的對稱軸對稱,求點
的對稱軸對稱,求點![]() 的坐標;
的坐標;
(2)求出以點![]() 為頂點的
為頂點的![]() 的“友好”拋物線
的“友好”拋物線![]() 的解析式;
的解析式;
(3)直接寫出![]() 與
與![]() 中
中![]() 同時隨
同時隨![]() 增大而增大的自變量
增大而增大的自變量![]() 的取值范圍.
的取值范圍.
【答案】(1)點D坐標為(4,4)
(2)拋物線![]() 的解析式為
的解析式為![]()
(3)![]()
【解析】
(1)根據拋物線![]() 的解析式可求得C點坐標及對稱軸,即可求得點D坐標.
的解析式可求得C點坐標及對稱軸,即可求得點D坐標.
(2)可設![]() 的交點式解析式,將頂點坐標代入即可求解.
的交點式解析式,將頂點坐標代入即可求解.
(3)畫圖像,根據圖像可得![]() 與
與![]() 中
中![]() 同時隨
同時隨![]() 增大而增大的自變量
增大而增大的自變量![]() 的取值范圍.
的取值范圍.
解:(1)∵點C是![]() 與
與![]() 軸交點
軸交點
∴點C坐標為(0,4)
將![]() 化成頂點式得:
化成頂點式得:![]()
∴頂點坐標為(2,-4),對稱軸為![]()
∵點![]() 與點
與點![]() 關于拋物線
關于拋物線![]() 的對稱軸對稱
的對稱軸對稱
∴點D坐標為(4,4).
(2)設![]() 解析式為:
解析式為:![]()
將(2,-4)代入解得![]()
∴![]() 的“友好”拋物線
的“友好”拋物線![]() 的解析式為
的解析式為![]() .
.
(3)畫出![]() 的圖像.
的圖像.

由圖像可知當![]() 時,
時,![]() 與
與![]() 中
中![]() 同時隨
同時隨![]() 增大而增大.
增大而增大.
故答案為:(1)點D坐標為(4,4)
(2)拋物線![]() 的解析式為
的解析式為![]()
(3)![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,點
,點![]() 為
為![]() 邊上一動點(與點
邊上一動點(與點![]() 不重合),連接
不重合),連接![]() 將
將![]() 的兩邊所在射線
的兩邊所在射線![]() 以點
以點![]() 為中心,順時針旋轉
為中心,順時針旋轉![]() 分別交射線
分別交射線![]() 于點
于點![]() .
.
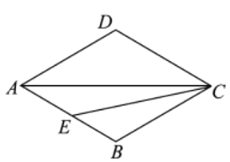
(1)依題意補全圖形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示線段![]() 與
與![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,BD為一條對角線,AD∥BC,AD=2BC,∠ABD=90°,E為AD的中點,連接BE.
(1)求證:四邊形BCDE為菱形;
(2)連接AC,若AC平分∠BAD,BC=2,求AC的長.
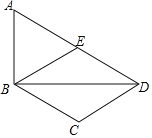
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形![]() 中,
中,![]() 是
是![]() 邊上的兩個動點,且
邊上的兩個動點,且![]() ,連接
,連接![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;⑤線段
;⑤線段![]() 的最小值是
的最小值是![]() .正確的個數有( )
.正確的個數有( )
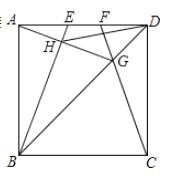
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市要進一批雞蛋進行銷售,有![]() 、
、![]() 兩家農場可供貨.為了比較兩家提供的雞蛋單個大小,超市分別對這兩家農場的雞蛋進行抽樣檢測,通過分析數據確定雞蛋的供貨商.
兩家農場可供貨.為了比較兩家提供的雞蛋單個大小,超市分別對這兩家農場的雞蛋進行抽樣檢測,通過分析數據確定雞蛋的供貨商.
(1)下列抽樣方式比較合理的是哪一種?請簡述原因.
①分別從![]() 、
、![]() 兩家提供的一箱雞蛋中拿出最上面的兩層(共40枚)雞蛋,并分別稱出其中每一個雞蛋的質量.
兩家提供的一箱雞蛋中拿出最上面的兩層(共40枚)雞蛋,并分別稱出其中每一個雞蛋的質量.
②分別從![]() 、
、![]() 兩家提供的一箱雞蛋中每一層隨機抽4枚(共40枚)雞蛋,并分別稱出其中每個雞蛋的質量.
兩家提供的一箱雞蛋中每一層隨機抽4枚(共40枚)雞蛋,并分別稱出其中每個雞蛋的質量.
(2)在用合理的方法抽出兩家提供的雞蛋各40枚后,分別稱出每個雞蛋的質量(單位:![]() ),結果如表所示(數據包括左端點不包括右端點).
),結果如表所示(數據包括左端點不包括右端點).
45~47 | 47~49 | 49~51 | 51~53 | 53~55 | |
| 2 | 8 | 15 | 10 | 5 |
| 4 | 6 | 12 | 14 | 4 |
①如果從這兩家農場提供的雞蛋中隨機拿一個,分別估計兩家雞蛋質量在![]() (單位:
(單位:![]() )范圍內的概率(數據包括左端點不包括右端點);
)范圍內的概率(數據包括左端點不包括右端點);
②如果你是超市經營者,試通過數據分析確定選擇哪家農場提供的雞蛋.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某公園內有一座古塔AB,在塔的北面有一棟建筑物,某日上午9時太陽光線與水平面的夾角為32°,此時塔在建筑物的墻上留下了高3米的影子CD.中午12時太陽光線與地面的夾角為45°,此時塔尖A在地面上的影子E與墻角C的距離為15米(B、E、C在一條直線上),求塔AB的高度.(結果精確到0.01米)
參考數據:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,![]() .
.
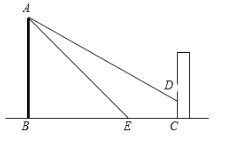
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() (
(![]() ,
,![]() 是常數,且
是常數,且![]() ),經過點
),經過點![]() ,
,![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(Ⅰ)求拋物線的解析式;
(Ⅱ)若點![]() 是射線
是射線![]() 上一點,過點
上一點,過點![]() 作
作![]() 軸的垂線,垂足為點
軸的垂線,垂足為點![]() ,交拋物線于點
,交拋物線于點![]() ,設
,設![]() 點橫坐標為
點橫坐標為![]() ,線段
,線段![]() 的長為
的長為![]() ,求出
,求出![]() 與
與![]() 之間的函數關系式,并寫出相應的自變量
之間的函數關系式,并寫出相應的自變量![]() 的取值范圍;
的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,當點![]() 在線段
在線段![]() 上時,設
上時,設![]() ,已知
,已知![]() ,
,![]() 是以
是以![]() 為未知數的一元二次方程
為未知數的一元二次方程![]() (
(![]() 為常數)的兩個實數根,點
為常數)的兩個實數根,點![]() 在拋物線上,連接
在拋物線上,連接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,求出
,求出![]() 值及點
值及點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,反比例函數y= ![]() 的圖象與一次函數y=x+b的圖象交
的圖象與一次函數y=x+b的圖象交
于點A(1,4)、點B(-4,n).

(1)求一次函數和反比例函數的解析式;
(2)求△OAB的面積;
(3)直接寫出一次函數值大于反比例函數值的自變量x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com