(2002•西城區)已知:在平面直角坐標系xoy中,點A(0,4),點B和點C在x軸上(點B在點C的左邊),點C在原點的右邊,作BE⊥AC,垂足為E(點E在線段AC上,且點E與點A不重合),直線BE與y軸交于點D.若BD=AC
(1)求點B的坐標;
(2)設OC長為m,△BOD的面積為S,求S與m的函數關系式,并寫出自變量m的取值范圍;
(3)當m=5時,求點D的坐標及sin∠BDO的值.
【答案】
分析:(1)分兩種情況,
①當B在原點左邊時,利用同角的余角相等,得到∠1=∠2,再證△AOC≌△BOD,得到OA=OB,因為A(0,4),所以B(-4,0);
②當B在原點右邊時,同①可證OA=OB=4,所以B(4,0);
(2)分兩種情況:當B在原點左側時,因為△AOC≌△BOD,所以OC=DO=m,即可得到S=

OB•OD=2m(0<m<4);當B在原點右側時,同理可得S=2m(m>4);
(3)因為m=5時,OD=OC=5,D只能在原點下方,所以D(0,-5),在Rt△BOD中,由勾股定理得BD,即可求出答案.
解答: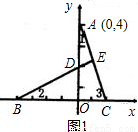
解:(1)根據題意,分兩種情況:
①當B在原點左邊時,如圖1,
∵∠AOC=∠BOD=90°,∠1+∠3=∠3+∠2,
∴∠1=∠2,
∵AC=BD,
∴△AOC≌△BOD,
∴OA=OB,
∵A(0,4),
∴B(-4,0);
②當B在原點右邊時,同①可證OA=OB=4,
∴B(4,0)
∴B(-4,0),或(4,0);
(2)當B在原點左側時,
∵△AOC≌△BOD,
∴OC=DO=m,
∴S=

OB•OD=2m(0<m<4),
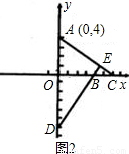
當B在原點右側時,同理可得S=2m,(m>4),
∴S=2m,(m>0,m≠4);
(3)當m=5時,OD=OC=5,
根據題意,D只能在原點下方,
∴D(0,-5),
在Rt△BOD中,由勾股定理得BD=
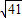
,
∴sin∠BDO=

.
點評:本題需仔細分析題意,利用勾股定理和全等三角形即可解決問題.

 OB•OD=2m(0<m<4);當B在原點右側時,同理可得S=2m(m>4);
OB•OD=2m(0<m<4);當B在原點右側時,同理可得S=2m(m>4); 解:(1)根據題意,分兩種情況:
解:(1)根據題意,分兩種情況: OB•OD=2m(0<m<4),
OB•OD=2m(0<m<4),
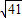 ,
, .
.

 有兩個實數解.求m的取值范圍;
有兩個實數解.求m的取值范圍; 有兩個實數解.求m的取值范圍;
有兩個實數解.求m的取值范圍;