
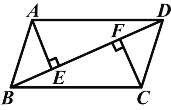
【題目】如圖,已知在四邊形ABCD中,AE⊥BD于E,CF⊥BD于F,AE=CF,BF=DE.求證:四邊形ABCD是平行四邊形.
【答案】見解析
【解析】
證明:證法一:∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
又∵AE⊥BD,CF⊥BD.
∴∠AEB=∠CFD=90°.
∵在△ABE和△CDF中,BE=DF,∠AEB=∠CFD,AE=CF,∴△ABE≌△CDF(SAS),∴AB=CD.
∵在△ADE和△CBF中,AE=CF,∠AED=∠BFC=90°,DE=BF,∴△ADE≌△CBF(SAS),∴AD=BC.
∴四邊形ABCD是平行四邊形(兩組對邊分別相等的四邊形是平行四邊形).
證法二:同證法一,得△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.同理可證:AD∥BC,
∴四邊形ABCD是平行四邊形(兩組對邊分別平行的四邊形是平行四邊形).
證法三:同證法一,得△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,∴AB∥CD.
∴四邊形ABCD是平行四邊形(一組對邊平行且相等的四邊形是平行四邊形).
證法四:連接AC,交BD于點O.
∵∠AEO=∠CFO=90°,∠AOE=∠COF,AE=CF.
∴△AOE≌△COF(AAS),∴AO=CO,EO=FO.
∵BF=DE,∴BE=DF,∴BE+EO=DF+FO,即BO=DO.
∴四邊形ABCD是平行四邊形(兩條對角線互相平分的四邊形是平行四邊形).


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=90°,以O為頂點、OB為一邊畫∠BOC,然后再分別畫出∠AOC與∠BOC的平分線OM、ON.
(1)在圖1中,射線OC在∠AOB的內部.
①若銳角∠BOC=30°,則∠MON= °;
②若銳角∠BOC=n°,則∠MON= °.
(2)在圖2中,射線OC在∠AOB的外部,且∠BOC為任意銳角,求∠MON的度數.
(3)在(2)中,“∠BOC為任意銳角”改為“∠BOC為任意鈍角”,其余條件不變,(圖3),求∠MON的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,點E、F分別在邊BC、CD上,且BE=DF=AD,聯結DE,聯結AF、BF分別與DE交于點G、P. 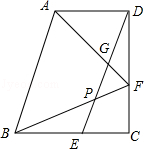
(1)求證:AB=BF;
(2)如果BE=2EC,求證:DG=GE.
查看答案和解析>>
科目:初中數學 來源: 題型:
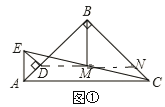
【題目】已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,點M是CE的中點,連接BM.
(1)如圖①,點D在AB上,連接DM,并延長DM交BC于點N,可探究得出BD與BM的數量關系為______________;
(2)如圖②,點D不在AB上,(1)中的結論還成立嗎?如果成立,請證明;如果不成立,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點G,點F是CD上一點,且滿足 ![]() ,連接AF并延長交⊙O于點E,連接AD、DE,若CF=3,AF=4.
,連接AF并延長交⊙O于點E,連接AD、DE,若CF=3,AF=4. 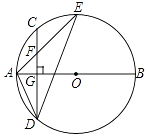
(1)求證:△ADF∽△AED;
(2)求FG的長;
(3)求tan∠E的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班計劃購買籃球和排球若干個,買4個籃球和3個排球需要410元;買2個籃球和5個排球需要310元.
(1)籃球和排球單價各是多少元?
(2)若兩種球共買30個,費用不超過1700元,籃球最多可以買多少個?
(3)如果購買這兩種球剛好用去520元,問有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】作圖題:
(1)如圖,在平面內有不共線的3個點A,B,C.
(a)作直線AB,射線AC,線段BC;
(b)延長BC到點D,使CD=BC,連接AD;
(c)作線段AB的中點E,連接CE;
(d)測量線段CE和AD的長度,直接寫出二者之間的數量關系_______.

(2) 有5個大小一樣的正方形制成如圖所示的拼接圖形(陰影部分),請你在圖中的拼接圖形上再接一個正方形,使新拼接成的圖形經過折疊后能成為一個封閉的正方體盒子.
注意:只需添加一個符合要求的正方形,并用陰影表示.
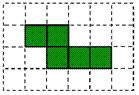
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
問題:如圖1,在平行四邊形ABCD中,E是AD上一點,AE=AB,∠EAB=60°,過點E作直線EF,在EF上取一點G,使得∠EGB=∠EAB,連接AG.
求證:EG =AG+BG.
小明同學的思路是:作∠GAH=∠EAB交GE于點H,構造全等三角形,經過推理解決問題.
參考小明同學的思路,探究并解決下列問題:
(1)完成上面問題中的證明;
(2)如果將原問題中的“∠EAB=60°”改為“∠EAB=90°”,原問題中的其它條件不變(如圖2),請探究線段EG、AG、BG之間的數量關系,并證明你的結論.

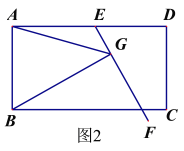
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com