
【題目】數(shù)學課上,林老師給出了下列方框中的一道題:
小聰和同桌小明討論后,得出如下解答:
(![]() )特殊情況,探索結論
)特殊情況,探索結論
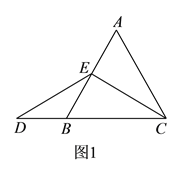
當點![]() 為
為![]() 的中點時,如圖
的中點時,如圖![]() ,確定線段
,確定線段![]() 與
與![]() 的大小關系,請你直接寫出結論:
的大小關系,請你直接寫出結論: ![]() ______
______ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
”或“![]() ”).
”).
(![]() )特例啟發(fā),解答問題
)特例啟發(fā),解答問題
解:題目中, ![]() 與
與![]() 的大小關系是
的大小關系是![]() __________
__________ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
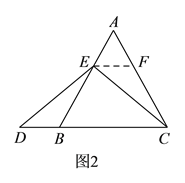
”或“![]() ”),理由如下:如圖
”),理由如下:如圖![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,(請你繼續(xù)完成接下來的解題過程).
,(請你繼續(xù)完成接下來的解題過程).
(![]() )拓展討論,設計新題
)拓展討論,設計新題
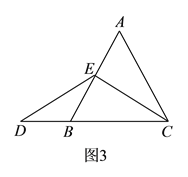
①互換林老師所給題的條件和結論,即:如圖![]() 在等邊三角形
在等邊三角形![]() 中,點
中,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,試確定線段
,試確定線段![]() 與
與![]() 的大小關系,并說明理由.
的大小關系,并說明理由.
②在等邊三角形![]() 中,點
中,點![]() 在直線
在直線![]() 上,點
上,點![]() 在直線
在直線![]() 上,且
上,且![]() ,若
,若![]() 的邊長為
的邊長為![]() ,
, ![]() ,求
,求![]() 的長為__________(請你直接寫出結果).
的長為__________(請你直接寫出結果).
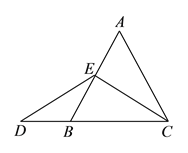
如圖,在等邊三角形![]() 中,點
中,點![]() 在
在![]()
上,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,
,
試確定線段![]() 與
與![]() 的大小關系,并說明理由.
的大小關系,并說明理由.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,見解析;(
,見解析;(![]() )①
)①![]() ;②
;②![]() 或
或![]() .
.
【解析】試題分析:(1)根據(jù)△ABC是等邊三角形,點E為AB的中點,即可得出CE⊥AB,進而得出∠ECD=∠D,即可得出線段ED與EC的大小關系;
(2)首先得出BE=CF,進而利用△DBE≌△EFC即可得出答案;
(3)①作![]() ,交
,交![]() 于點
于點![]() ,可知
,可知![]() 為等邊三角形,進而證明
為等邊三角形,進而證明![]() ≌
≌![]() ,即可得出
,即可得出![]() ;
;
②分點D在CB的延長線上、在BC的延長線上兩種情況進行討論即可得.
試題解析:(![]() )
)![]() .
.
∵![]() 為等邊三角形,
為等邊三角形, ![]() 是
是![]() 中點,∴
中點,∴![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )
)![]()
在等邊![]() 中,
中, ![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
同理![]() ,
,
又在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
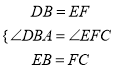 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )①作
)①作![]() ,交
,交![]() 于點
于點![]() ,
,
則可知![]() 為等邊三角形,
為等邊三角形,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() 和
和![]() 中,
中,
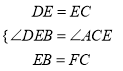 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() .
.
②![]() ,
,
∴![]() 或
或![]() .
.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖是一個用來盛爆米花的圓錐形紙杯,紙杯開口的直徑 EF 長為10cm,母線OE(OF)長為10cm,在母線OF 上的點A 處有一塊爆米花殘渣且FA=2cm,一只螞蟻從杯口的點E 處沿圓錐表面爬行到A 點,則此螞蟻爬行的最短距離為 cm.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在正方形網(wǎng)格中,每個小正方形的邊長均為1個單位長度,△ABC的三個頂點的位置如圖所示,現(xiàn)將△ABC平移,使點A變換為點A′,點B′、C′分別是B、C的對應點.

(1)請畫出平移后的△A′B′C′,并求△A′B′C′的面積;
(2)若連接AA′,CC′,則這兩條線段之間的關系是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
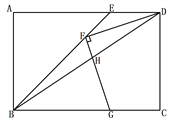
【題目】如圖,矩形ABCD中,BE平分∠ABC交AD于點E,F(xiàn)為BE上一點,連接DF,過F作FG⊥DF交BC于點G,連接BD交FG于點H,若FD = FG, ![]() ,BG = 4,則GH的長為__________.
,BG = 4,則GH的長為__________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲乙兩個同學分解因式x2+ax+b時,甲看錯了b,分解結果為(x+2)(x+4),乙看錯了a,分解結果為(x+1)(x+9),則2a+b=_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
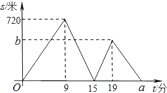
【題目】甲、乙二人從學校出發(fā)去科技館,甲步行一段時間后,乙騎自行車沿相同路線行進,兩人均勻速前行,他們的路程差s(米)與甲出發(fā)時間t(分)之間的函數(shù)關系如圖所示.下列說法:①乙先到達科技館;②乙的速度是甲速度的2.5倍;③b=460;④a=25.其中正確的是______(填序號).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知關于x、y的方程組![]()
(1)求方程組的解(用含m的代數(shù)式表示);
(2)若方程組的解滿足條件x<0,且y<0,求m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,∠ABD和∠BDC的平分線交于E,BE交CD于點F,∠1+∠2=90°.

(1)試說明:AB∥CD;
(2)若∠2=25°,求∠BFC的度數(shù).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com