
【題目】如圖,墻面OC與地面OD垂直,一架梯子AB長5米,開始時梯子緊貼墻面,梯子頂端A沿墻面勻速每分鐘向下滑動1米,x分鐘后點A滑動到點A′,梯子底端B沿地面向左滑動到點B′,OB′=y米,滑動時梯子長度保持不變.
(1)當x=1時,y= 米;
(2)求y關于x的函數關系式,并寫出自變量x的取值范圍;
(3)研究(2)中函數圖象及其性質.
①填寫下表,并在所給的坐標系中畫出函數圖象;
②如果點P(x,y)在(2)中的函數圖象上,求證:點P到點Q(5,0)的距離是定值;
(4)梯子底端B沿地面向左滑動的速度是
A.勻速 B.加速 C.減速 D.先減速后加速.

【答案】(1)3(2)![]() (3)①表格見解析②P到點Q(5,0)的距離是定值(4)C
(3)①表格見解析②P到點Q(5,0)的距離是定值(4)C
【解析】
試題分析:(1)在Rt△A′OB′中,根據勾股定理求出OB′即可.
(2)在Rt△A′OB′中,根據勾股定理即可解決問題,再根據題意寫出自變量的取值范圍.
(3)①先列表,再畫出圖象即可.②利用兩點間距離公式即可解決問題.
(4)如圖2中,在半徑OQ上取AB=BC,過A、B、C作x軸的垂線交圓弧于D、E、F,作DM⊥BE,EN⊥CF,延長DE交CF于G,只要證明EM>FN即可解決問題.
試題解析:(1)x=1時,A′B=5﹣1=4,A′B′=5,
∵∠O=90°,
∴y=OB′=![]() =3.
=3.
故答案為3.
(2)![]() ,(0≤x≤5).
,(0≤x≤5).
(3)①填表:
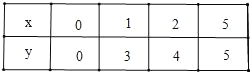
②圖象如圖所示:
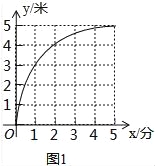
∵![]() ,
,
∴y2+(5﹣x)2=52,
即PQ2=PR2+RQ2=25,
∴PQ=5,
∴P到點Q(5,0)的距離是定值
(4)與(3)可知,函數圖象是以Q為圓心的圓弧,
如圖2中,在半徑OQ上取AB=BC,過A、B、C作x軸的垂線交圓弧于D、E、F,作DM⊥BE,EN⊥CF,延長DE交CF于G.那么GN=EM,
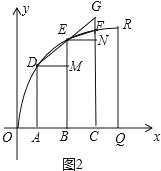
∵GN>FN,
∴EM>FN,
即點A移動的距離大于點B移動的距離,
∴是減速,
故選C.


科目:初中數學 來源: 題型:
【題目】小明解不等式![]() 的過程如圖,請指出他解答過程中錯誤步驟的序號,并寫出正確的解答過程.
的過程如圖,請指出他解答過程中錯誤步驟的序號,并寫出正確的解答過程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括號,得3+3x-4x+1≤1.②
移項,得3x-4x≤1-3-1.③
合并同類項,得-x≤-3.④
兩邊都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,長方形OABC的邊OA在數軸上,O為原點,長方形OABC的面積為12,OC邊長為3.
(1)數軸上點A表示的數為
(2)將長方形OABC沿數軸水平移動,移動后的長方形記為O′A′B′C′,移動后的長方形O′A′B′C′與原長方形OABC重疊部分(如圖2中陰影部分)的面積記為S. ①當S恰好等于原長方形OABC面積的一半時,數軸上點A′表示的數為 .
②設點A的移動距離AA′=x.
ⅰ.當S=4時,x=;
ⅱ.D為線段AA′的中點,點E在線段OO′上,且OE= ![]() OO′,當點D,E所表示的數互為相反數時, x=
OO′,當點D,E所表示的數互為相反數時, x=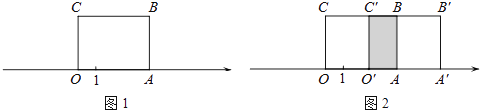
查看答案和解析>>
科目:初中數學 來源: 題型:
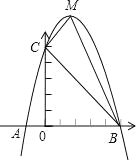
【題目】已知:如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,其中A點坐標為(﹣1,0),點C(0,5),另拋物線經過點(1,8),M為它的頂點.
(1)求拋物線的解析式;
(2)求△MCB的面積![]() .
.
(3)在坐標軸上,是否存在點N,滿足△BCN為直角三角形?如存在,請直接寫出所有滿足條件的點N.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于n的函數s=an2+bn(n為自然數),當n=9時,s<0;當n=10時,s>0.則n取( )時,s的值最小.
A.3B.4C.5D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有理數a,b在數軸上的表示如圖所示,則下列結論中:①ab<0,② ![]() ,③a+b<0, ④a﹣b<0,⑤a<|b|,⑥﹣a>﹣b,正確的有( )
,③a+b<0, ④a﹣b<0,⑤a<|b|,⑥﹣a>﹣b,正確的有( )![]()
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com