

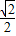 AD,DG=GC=
AD,DG=GC=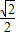 CD,CF=BF=
CD,CF=BF=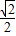 BC,AE=BE=
BC,AE=BE=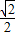 AB,推出EF=FG=GH=EH,根據正方形的判定推出四邊形EFGH是正方形即可;
AB,推出EF=FG=GH=EH,根據正方形的判定推出四邊形EFGH是正方形即可; AB,DG=
AB,DG= CD,平行四邊形的性質得出AB=CD,求出∠HDG=90°+a=∠HAE,根據SAS證△HAE≌△HDG,根據全等三角形的性質即可得出HE=HG;
CD,平行四邊形的性質得出AB=CD,求出∠HDG=90°+a=∠HAE,根據SAS證△HAE≌△HDG,根據全等三角形的性質即可得出HE=HG;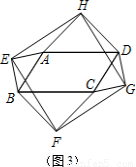 ②證明:∵△AEB和△DGC是等腰直角三角形,
②證明:∵△AEB和△DGC是等腰直角三角形, AB,DG=
AB,DG= CD,
CD,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
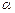 (0°<
(0°<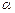 <90°),
<90°),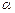 的代數式表示∠HAE= ;(1分)
的代數式表示∠HAE= ;(1分)
查看答案和解析>>
科目:初中數學 來源:2011-2012年江蘇省蘇州張家港市第二中學八年級上學期期中考試數學卷 題型:解答題
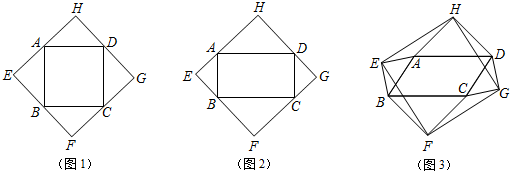
(本題10分) 以四邊形ABCD的邊AB、BC、CD、DA為斜邊分別向外側作等腰直角三角形,直角頂點分別為E、F、G、H,順次連結這四個點得四邊形EFGH.如圖1,當四邊形ABCD為正方形時,我們發現四邊形EFGH是正方形;
【小題1】(1)如圖2,當四邊形ABCD為矩形時,則四邊形EFGH的形狀是 ;(1分)
【小題2】(2)如圖3,當四邊形ABCD為一般平行四邊形時,設∠ADC= (0°<
(0°< <90°),
<90°),
【小題3】① 試用含 的代數式表示∠HAE= ;(1分)
的代數式表示∠HAE= ;(1分)
【小題4】② 求證:HE=HG;(4分)③ 四邊形EFGH是什么四邊形?并說明理由.(4分)
查看答案和解析>>
科目:初中數學 來源:2011-2012年江蘇省蘇州張家港市八年級上學期期中考試數學卷 題型:解答題
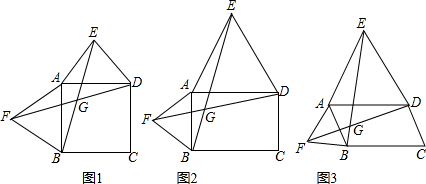
(本題10分) 以四邊形ABCD的邊AB、BC、CD、DA為斜邊分別向外側作等腰直角三角形,直角頂點分別為E、F、G、H,順次連結這四個點得四邊形EFGH.如圖1,當四邊形ABCD為正方形時,我們發現四邊形EFGH是正方形;
1.(1)如圖2,當四邊形ABCD為矩形時,則四邊形EFGH的形狀是 ;(1分)
2.(2)如圖3,當四邊形ABCD為一般平行四邊形時,設∠ADC= (0°<
(0°< <90°),
<90°),
3.① 試用含 的代數式表示∠HAE=
;(1分)
的代數式表示∠HAE=
;(1分)
4.② 求證:HE=HG;(4分)③ 四邊形EFGH是什么四邊形?并說明理由.(4分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com