
【題目】已知AM∥CN,點B為平面內一點,AB⊥BC于B.

(1)如圖1,直接寫出∠A和∠C之間的數量關系___;
(2)如圖2,過點B作BD⊥AM于點D,求證:∠ABD=∠C;
(3)如圖3,在(2)問的條件下,點E. F在DM上,連接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度數.
【答案】(1)∠A+∠C=90°;(2)見解析;(3)105°.
【解析】
(1)根據平行線的性質以及直角三角形的性質進行解答即可;
(2)先過點B作BG∥DM,根據同角的余角相等,得出∠ABD=∠CBG,再根據平行線的性質,得出∠C=∠CBG,即可得到∠ABD=∠C;
(3)先過點B作BG∥DM,根據角平分線的定義,得出∠ABF=∠GBF,再設∠DBE=α,∠ABF=β,根據∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根據AB⊥BC,可得β+β+2α=90°,最后解方程組即可得到∠ABE=15°,進而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.
(1)如圖1,∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
故答案為∠A+∠C=90°;
(2)如圖2,過點B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如圖3,過點B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
設∠DBE=α,∠ABF=β,
則∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
在△BCF中,由∠CBF+∠BFC+∠BCF=180°,
可得 (2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②聯立方程組,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.



 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
【題目】“五一”期間,某商場推出“購物滿額即可抽獎”活動.商場在抽獎箱中裝有1個紅球、2個黃球、3個白球、8個黑球,每個球除顏色外都相同,紅球、黃球、白球分別代表一、二、三等獎,黑球代表謝謝參與.獲得抽獎機會的顧客每次從箱子中摸出一個球,按相應顏色對應等級兌換獎品,每次所摸得球再放回抽獎箱,搖勻后由下一位顧客抽獎.已知小明獲得1次抽獎機會.
(1)小明是否一定能中獎___________;(填是、否)
(2)求出小明抽到一等獎的概率;
(3)在這個活動中,中獎和沒中獎的機會相等嗎?為什么?如果不相等,可以如何改變球的個數,使中獎和沒中獎的機會相等?(只寫一種即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若點P從點A出發,以每秒2cm的速度沿折線![]() 運動,設運動時間為
運動,設運動時間為![]() 秒。
秒。
(1)AC=______cm;
(2)若點P恰好在∠ABC的角平分線上,求此時![]() 的值;
的值;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了從甲、乙兩人中選拔一人參加射擊比賽,現對他們的射擊成績進行了測試,5次打靶命中的環數如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)將下表填寫完整:
平均數 | 中位數 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根據以上信息,若你是教練,你會選擇誰參加射擊比賽,理由是什么?
(3)若乙再射擊一次,命中8環,則乙這六次射擊成績的方差會 .(填“變大”或“變小”或“不變”)
查看答案和解析>>
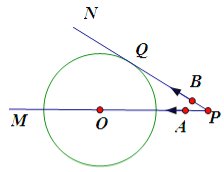
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙![]() 的半徑為9cm,射線
的半徑為9cm,射線![]() 經過點
經過點![]() ,OP=15 cm,射線
,OP=15 cm,射線![]() 與⊙
與⊙![]() 相切于點
相切于點![]() .動點
.動點![]() 自P點以
自P點以![]() cm/s的速度沿射線
cm/s的速度沿射線![]() 方向運動,同時動點
方向運動,同時動點![]() 也自P點以2cm/s的速度沿射線
也自P點以2cm/s的速度沿射線![]() 方向運動,則它們從點
方向運動,則它們從點![]() 出發 s后
出發 s后![]() 所在直線與⊙
所在直線與⊙![]() 相切.
相切.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了更好地開展“陽光體育一小時”活動,對本校學生進行了“寫出你最喜歡的體育活動項目(只寫一項)”的隨機抽樣調查,下面是根據得到的相關數據繪制的統計圖的一部分.
抽樣調查學生最喜歡的運動項目的人數統計圖 各運動項目的喜歡人數占抽樣總人數百分比統計圖

請根據以上信息解答下列問題:
(1)該校對________名學生進行了抽樣調查;
(2)請將圖1和圖2補充完整;
(3)圖2中跳繩所在的扇形對應的圓心角的度數是________;
(4)若該校共有2400名同學,請利用樣本數據估計全校學生中最喜歡跳繩運動的人數約為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AD是弦,∠A=22.5°,延長AB到點C,使得∠ACD=45°.
(1)求證:CD是⊙O的切線.
(2)若AB=2![]() ,求OC的長.
,求OC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:如圖,在△![]() 中,把
中,把![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得到
得到![]() ,把
,把![]() 繞點
繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 得到
得到![]() ,連接
,連接![]() ,當
,當![]() 時,我們稱△
時,我們稱△![]() 是△
是△![]() 的“旋補三角形”,△
的“旋補三角形”,△![]() 邊
邊![]() 上的中線
上的中線![]() 叫做
叫做![]() 的“旋補中線”,點
的“旋補中線”,點![]() 叫做“旋補中心”.
叫做“旋補中心”.
⑴ 特例感知:在如圖、如圖中,![]() 是
是![]() 的“旋補三角形”,
的“旋補三角形”,![]() 是
是![]() 的“旋補中線”.
的“旋補中線”.
① 如圖,當![]() 為等邊三角形時,
為等邊三角形時,![]() 與
與![]() 的數量關系為
的數量關系為![]() =
= ![]() ;
;
② 如圖,當![]() ,
,![]() 時,則
時,則![]() 長為 .
長為 .
⑵ 精確作圖:如圖,已知在四邊形![]() 內部存在點
內部存在點![]() ,使得
,使得![]() 是
是![]() 的“旋補三角形”(點D的對應點為點A,點C的對應點為點B),請用直尺和圓規作出點
的“旋補三角形”(點D的對應點為點A,點C的對應點為點B),請用直尺和圓規作出點![]() (要求:保留作圖痕跡,不寫作法和證明)
(要求:保留作圖痕跡,不寫作法和證明)
⑶ 猜想論證:在如圖中,當△![]() 為任意三角形時,猜想
為任意三角形時,猜想![]() 與
與![]() 的數量關系,并給予證明.
的數量關系,并給予證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖像經過點
的圖像經過點![]() .
.
(![]() )求該二次函數的關系式.
)求該二次函數的關系式.
(![]() )證明:無論
)證明:無論![]() 取何值,函數值
取何值,函數值![]() 總不等于
總不等于![]() .
.
(![]() )將該拋物線先向___________(填“左”或“右”)平移___________個單位,再向___________(填“上”或“下”)平移___________個單位,使得該拋物線的頂點為原點.
)將該拋物線先向___________(填“左”或“右”)平移___________個單位,再向___________(填“上”或“下”)平移___________個單位,使得該拋物線的頂點為原點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com