
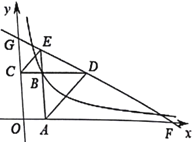
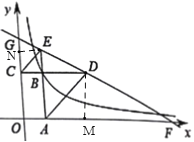
【題目】如圖,矩形OABC在直角坐標(biāo)系中,延長AB至點(diǎn)E使得BE=BC連接CE,過A作AD//CE交CB延長線于點(diǎn)D,直線DE分別交x軸、y軸于F、G點(diǎn),若EG:DF=1:4,且△BCE與△BAD面積之和為![]() ,則過點(diǎn)
,則過點(diǎn)![]() 的雙曲線
的雙曲線![]() 中
中![]() 的值為____.
的值為____.
【答案】3
【解析】
如圖,過點(diǎn)E作EN⊥y軸于N,過點(diǎn)D作DM⊥x軸于M,設(shè)B(x、y),由矩形的性質(zhì)及BE=BC可得△BCE是等腰直角三角形,可得∠BCE=45°,根據(jù)平行線的性質(zhì)可得∠ADC=∠BCE=45°,可得△ABD是等腰直角三角形,可得BD=AB=y,根據(jù)平行線的性質(zhì)可得∠NEG=∠BDE=∠MFD,可證明△NEG∽△MFD,△BDE∽△MFD,根據(jù)相似三角形的性質(zhì)可得y2=4x2,根據(jù)△BCE與△BAD面積之和為![]() 可得x2+y2=
可得x2+y2=![]() ,進(jìn)而求出xy的值即可得答案.
,進(jìn)而求出xy的值即可得答案.
如圖,過點(diǎn)E作EN⊥y軸于N,過點(diǎn)D作DM⊥x軸于M,設(shè)B(x、y),
∴BC=x,AB=y,
∵BE=BC,四邊形OABC是矩形,
∴△BCE是等腰直角三角形,
∴∠BCE=45°,
∵AD//CE,
∴∠ADC=∠BCE=45°,
∴△ABD是等腰直角三角形,
∴BD=AB=y,
∵EN⊥y軸,DM⊥x軸,
∴四邊形GCBE、BAMD都是正方形,
∴EG=BC=x,DM=AB=y,
∵∠GNE=∠DCG=∠FOG=90°,
∴EG//CD//OF,
∴∠NEG=∠BDE=∠MFD,
∴△NEG∽△MFD,△BDE∽△MFD,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴y2=4x2,
∵△BCE與△BAD面積之和為![]() ,
,
∴![]() x2+
x2+![]() y2=
y2=![]() ,即x2+y2=
,即x2+y2=![]() ,
,
∴x2+4x2=![]() ,
,
解得:x2=![]() ,
,
∴y2=4x2=6,
∴(xy)2=9,
∵點(diǎn)B在雙曲線![]() 圖象上,且圖象在第一象限,
圖象上,且圖象在第一象限,
∴k=xy=3,
故答案為:3


 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一個兩位數(shù)中,個位數(shù)字比十位數(shù)字大1,則稱這個兩位數(shù)為“遞增數(shù)”.例如56就是一個“遞增數(shù)”,現(xiàn)有2,3,4,5四個數(shù)字.
(1)若先抽出的數(shù)字3作為十位數(shù),再從其余3個數(shù)字隨機(jī)抽出1個數(shù)字為個位數(shù),組成的兩位數(shù)恰為“遞增數(shù)”的概率為________.
(2)先從四個數(shù)中隨機(jī)抽出一個數(shù)作為十位數(shù),再從其余3個數(shù)字隨機(jī)抽出1個數(shù)字為個位數(shù).組成的兩位數(shù)恰為“遞增數(shù)”的概率是多少?請用列表或畫樹狀圖的方法分析.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 邊上一動點(diǎn)(與點(diǎn)
邊上一動點(diǎn)(與點(diǎn)![]() 不重合),連接
不重合),連接![]() 將
將![]() 的兩邊所在射線
的兩邊所在射線![]() 以點(diǎn)
以點(diǎn)![]() 為中心,順時針旋轉(zhuǎn)
為中心,順時針旋轉(zhuǎn)![]() 分別交射線
分別交射線![]() 于點(diǎn)
于點(diǎn)![]() .
.
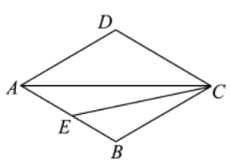
(1)依題意補(bǔ)全圖形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示線段![]() 與
與![]() 之間的數(shù)量關(guān)系,并證明.
之間的數(shù)量關(guān)系,并證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=90°,點(diǎn)D是邊BC上的動點(diǎn),連接AD,點(diǎn)C關(guān)于直線AD的對稱點(diǎn)為點(diǎn)E,射線BE與射線AD交于點(diǎn)F.


(1)在圖1中,依題意補(bǔ)全圖形;
(2)記![]() (
(![]() ),求
),求![]() 的大小;(用含
的大小;(用含![]() 的式子表示)
的式子表示)
(3)若△ACE是等邊三角形,猜想EF和BC的數(shù)量關(guān)系,并證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() 為拋物線
為拋物線![]() 上一動點(diǎn),以
上一動點(diǎn),以![]() 為頂點(diǎn),且經(jīng)過原點(diǎn)
為頂點(diǎn),且經(jīng)過原點(diǎn)![]() 的拋物線,記作“
的拋物線,記作“![]() ”,設(shè)其與
”,設(shè)其與![]() 軸另一交點(diǎn)為
軸另一交點(diǎn)為![]() ,點(diǎn)
,點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
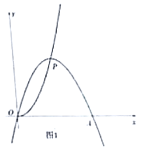
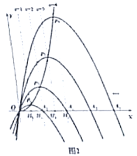
(1)①當(dāng)![]() 為直角三角形時,
為直角三角形時,![]() ________;
________;
②當(dāng)![]() 為等邊三角形時,求此時“
為等邊三角形時,求此時“![]() ”的解析式;
”的解析式;
(2)若![]() 點(diǎn)的橫坐標(biāo)分別為1,2,3,……
點(diǎn)的橫坐標(biāo)分別為1,2,3,……![]() (
(![]() 為正整數(shù))時,拋物線“
為正整數(shù))時,拋物線“![]() ”,分別記作“
”,分別記作“![]() ”,“
”,“![]() ”…“
”…“![]() ”,設(shè)其與
”,設(shè)其與![]() 軸另一交點(diǎn)分別為
軸另一交點(diǎn)分別為![]() ,
,![]() ,
,![]() …
…![]() ,過
,過![]() ,
,![]() ,
,![]() ,…,
,…,![]() 作
作![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() ,
,![]() ,
,![]() ,…,
,…,![]() .
.
①![]() 的坐標(biāo)為________,
的坐標(biāo)為________,![]() ________;(用含
________;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
②當(dāng)![]() 時,求
時,求![]() 的值;
的值;
③是否存在這樣的![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料:
對于任意正實(shí)數(shù)a、b,
∵![]() ,
,
![]()
![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() 時,等號成立.
時,等號成立.
結(jié)論:在![]() 均為正實(shí)數(shù))中,若
均為正實(shí)數(shù))中,若![]() 為定值
為定值![]() 則
則![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() 時,a+b有最小值
時,a+b有最小值![]() .
.
拓展:對于任意正實(shí)數(shù)![]() ,都有
,都有![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() 時,等號成立.
時,等號成立.
在![]() (a、b、c均為正實(shí)數(shù))中,若
(a、b、c均為正實(shí)數(shù))中,若![]() 為定值
為定值![]() ,則
,則![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() 時,
時,![]() 有最小值
有最小值![]()
例如:![]() 則
則![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() ,即
,即![]() 時等號成立.
時等號成立.
又如:若![]() 求
求![]() 的最小值時,因?yàn)?/span>
的最小值時,因?yàn)?/span>![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時等號成立,故當(dāng)
時等號成立,故當(dāng)![]() 時,
時,![]() 有最小值
有最小值![]() .
.
根據(jù)上述材料,解答下列問題:
(1)若a為正數(shù),則當(dāng)a=______時,代數(shù)式![]() 取得最小值,最小值為_____;
取得最小值,最小值為_____;
(2)已知函數(shù)![]() 與函數(shù)
與函數(shù)![]() ,求函數(shù)
,求函數(shù)![]() 的最小值及此時
的最小值及此時![]() 的值;
的值;
(3)我國某大型空載機(jī)的一次空載運(yùn)輸成本包含三部分:一是基本運(yùn)輸費(fèi)用,共8100元;二是飛行耗油,每一百公里1200元;三是飛行報耗費(fèi)用,飛行報耗費(fèi)用與路程(單位:百公里)的平方成正比,比例系數(shù)為0.04,設(shè)該空載機(jī)的運(yùn)輸路程為![]() 百公里,則該空載機(jī)平均每一百公里的運(yùn)輸成本
百公里,則該空載機(jī)平均每一百公里的運(yùn)輸成本![]() 最低為多少?
最低為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,已知拋物線![]() (
(![]() 、
、![]() 為常數(shù))的頂點(diǎn)為
為常數(shù))的頂點(diǎn)為![]() ,等腰直角三角形
,等腰直角三角形![]() 的頂點(diǎn)
的頂點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,直角頂點(diǎn)
,直角頂點(diǎn)![]() 在第四象限.
在第四象限.
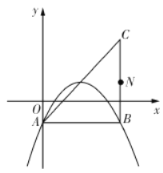
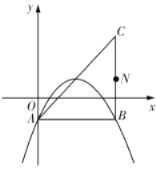
(1)如圖,若該拋物線經(jīng)過![]() 、
、![]() 兩點(diǎn),求該拋物線的函數(shù)表達(dá)式;
兩點(diǎn),求該拋物線的函數(shù)表達(dá)式;
(2)平移(1)中的拋物線,使頂點(diǎn)![]() 在直線
在直線![]() 上滑動,且與
上滑動,且與![]() 交于另一點(diǎn)
交于另一點(diǎn)![]() .
.
①若點(diǎn)![]() 在直線
在直線![]() 下方,且為平移前(1)中的拋物線上的點(diǎn),當(dāng)以
下方,且為平移前(1)中的拋物線上的點(diǎn),當(dāng)以![]() 、
、![]() 、
、![]() 三點(diǎn)為頂點(diǎn)的三角形是等腰直角三角形時,求出所有符合條件的點(diǎn)
三點(diǎn)為頂點(diǎn)的三角形是等腰直角三角形時,求出所有符合條件的點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD內(nèi)接于⊙O,∠BAD =90°,AC是對角線.點(diǎn)E在BC的延長線上,且∠CED =∠BAC.
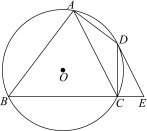
(1)判斷DE與⊙O的位置關(guān)系,并說明理由;
(2)BA與CD的延長線交于點(diǎn)F,若DE∥AC,AB=4,AD =2,求AF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,矩形紙片![]() 滿足
滿足![]() .將此矩形紙片按下列順序折疊,則圖4中
.將此矩形紙片按下列順序折疊,則圖4中![]() 的長為___________________(用含
的長為___________________(用含![]() 的代數(shù)式表示).
的代數(shù)式表示).
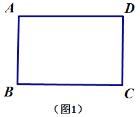
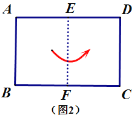


查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com