
【題目】如圖,正六邊形ABCDEF內接于⊙O,BE是⊙O的直徑,連接BF,延長BA,過F作FG⊥BA,垂足為G.
(1)求證:FG是⊙O的切線;
(2)已知FG=2![]() ,求圖中陰影部分的面積.
,求圖中陰影部分的面積.

【答案】(1)見解析;(2) 圖中陰影部分的面積為![]() .
.
【解析】
(1)連接OF,AO,根據題意可得∠ABF=∠AFB=∠EBF=30°,再利用OB=OF,證明AB∥OF,即可解答
(2)先利用等弧對等角求出△AOF是等邊三角形,再證明S△ABF=S△AOF,即可解答
(1)證明:連接OF,AO,
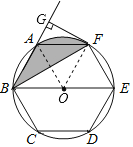
∵AB=AF=EF,
∴![]() ,
,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切線;
(2)解:∵![]() ,
,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等邊三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2![]() ,
,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴圖中陰影部分的面積=![]() .
.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:
【題目】某學校為九年級數學競賽獲獎選手購買以下三種獎品,其中小筆記本每本5元,大筆記本每本7元,鋼筆每支10元,購買的大筆記本的數量是鋼筆數量的2倍,共花費346元,若使購買的獎品總數最多,則這三種獎品的購買數量各為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應國家的一帶一路經濟發展戰略,樹立品牌意識,我市質檢部分別對A、B、C、D四個廠家生產的同種型號的零件共2000件進行合格率檢測,通過檢測得出C廠家的合格率為95%,并根據檢測數據繪制了如圖1、圖2兩幅不完整的統計圖:
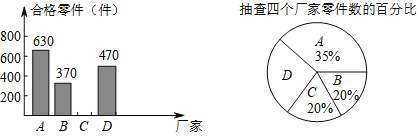
(1)抽查D廠家的零件為 件,扇形統計圖中D廠家對應的圓心角為 度;
(2)抽查C廠家的合格率零件為 件,并將圖1補充完整;
(3)通過計算說明A、C兩廠家誰的合格率更高?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,將一個矩形紙片![]() 放置在平面直角坐標系中,點
放置在平面直角坐標系中,點![]() 的坐標是
的坐標是![]() ,點
,點![]() 的坐標是
的坐標是![]() ,點
,點![]() 的坐標是
的坐標是![]() .點
.點![]() 是
是![]() 的中點,在
的中點,在![]() 上取一點
上取一點![]() ,將
,將![]() 沿
沿![]() 翻折,使點
翻折,使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處.
處.
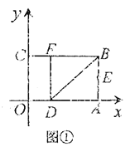
(Ⅰ)求點![]() 、
、![]() 的坐標;
的坐標;
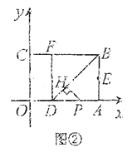
(Ⅱ)如圖②,若點![]() 是線段
是線段![]() 上的一個動點(點
上的一個動點(點![]() 不與點
不與點![]() ,
,![]() 重合),過點
重合),過點![]() 作
作![]() 于
于![]() ,設
,設![]() 的長為
的長為![]() ,
,![]() 的面積為
的面積為![]() ,試用關于
,試用關于![]() 的代數式表示
的代數式表示![]() ;
;
(Ⅲ)在![]() 軸、
軸、![]() 軸上分別存在點
軸上分別存在點![]() 、
、![]() ,使得四邊形
,使得四邊形![]() 的周長最小,請直接寫出四邊形
的周長最小,請直接寫出四邊形![]() 的周長最小值.
的周長最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
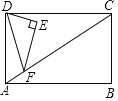
【題目】如圖,在矩形ABCD中,AB=4,∠DCA=30°,點F是對角線AC上的一個動點,連接DF,以DF為斜邊作∠DFE=30°的直角三角形DEF,使點E和點A位于DF兩側,點F從點A到點C的運動過程中,點E的運動路徑長是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
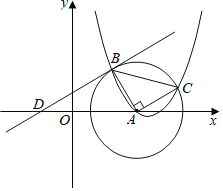
【題目】如圖,已知![]() 的圓心為點
的圓心為點![]() ,拋物線
,拋物線![]() 過點
過點![]() ,與
,與![]() 交于
交于![]() 兩點,連接
兩點,連接![]() 、
、![]() ,且
,且![]() ,
,![]() 兩點的縱坐標分別是2、1.
兩點的縱坐標分別是2、1.
(1)請直接寫出點![]() 的坐標,并求
的坐標,并求![]() 的值;
的值;
(2)直線![]() 經過點
經過點![]() ,與
,與![]() 軸交于點
軸交于點![]() .點
.點![]() (與點
(與點![]() 不重合)在該直線上,且
不重合)在該直線上,且![]() ,請判斷點
,請判斷點![]() 是否在此拋物線上,并說明理由;
是否在此拋物線上,并說明理由;
(3)如果直線![]() 與
與![]() 相切,請直接寫出滿足此條件的直線解析式.
相切,請直接寫出滿足此條件的直線解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線![]() 經過點A(-3,4).
經過點A(-3,4).
(1)求b的值;
(2)過點A作![]() 軸的平行線交拋物線于另一點B,在直線AB上任取一點P,作點A關于直線OP的對稱點C;
軸的平行線交拋物線于另一點B,在直線AB上任取一點P,作點A關于直線OP的對稱點C;
①當點C恰巧落在![]() 軸時,求直線OP的表達式;
軸時,求直線OP的表達式;
②連結BC,求BC的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解九年級學生的體育達標情況,隨機抽取![]() 名九年級學生進行體育達標項目測試,測試成績如下表,請根據表中的信息,解答下列問題:
名九年級學生進行體育達標項目測試,測試成績如下表,請根據表中的信息,解答下列問題:
測試成績(分) |
|
|
|
|
|
人數(人) |
|
|
|
|
|
(1)該校九年級有![]() 名學生,估計體育測試成績為
名學生,估計體育測試成績為![]() 分的學生人數;
分的學生人數;
(2)該校體育老師要對本次抽測成績為![]() 分的甲、乙、丙、丁
分的甲、乙、丙、丁![]() 名學生進行分組強化訓練,要求兩人一組,求甲和乙恰好分在同一組的概率.(用列表或樹狀圖方法解答)
名學生進行分組強化訓練,要求兩人一組,求甲和乙恰好分在同一組的概率.(用列表或樹狀圖方法解答)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com