【題目】某商場服裝柜在銷售中發現：某品牌童裝平均每天可售出20件，每件盈利40元.為了迎接“六一”國際兒童節，商場決定采取適當的降價措施，擴大銷售量，增加盈利，盡量減少庫存.經市場調查發現：如果每件童裝降價1元，那么平均每天就可多售出2件.假設商場降價
元，
（1）降價元后，每一件童裝的利潤為___________（元），每天可以賣出去的童裝件數為____________（件）（用含的代數式表示）；
（2）若銷售該童裝每天盈利要達到1200元，則每件童裝應該降價多少元？
【答案】（1）40-
，20+
；（2）20
【解析】
（1）根據“利潤=售價-進價”和“每件童裝降價1元，那么平均每天就可多售出2件”，可得到結果；
（2）根據利潤=銷售量×單件利潤列出方程即可求解；
（1）根據題意可知：原來每天可售出20件，每件盈利40元，當降價元后，每件盈利變為（40-）元，又因為每件童裝降價1元，那么平均每天就可多售出2件，降價后的銷售數量為（20+）件．
（2）由于每天總盈利利潤=每天銷售量×單件利潤，根據（1）中的數據可列方程：
，
整理得：
，
解方程得：
或
，
∵題目要求盡量減少庫存，當時，賣出的多，庫存比少，
∴要使每天盈利要達到1200元，則每件童裝應該降價20元
中考解讀考點精練系列答案科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示，有以下結論：①abc＞0，②3a+c＜0，③a﹣b+c＞0，④4a+2b+c＞0，⑤若點（﹣2，y1）和（﹣
，y2）在該圖象上，則y1＞y2，其中正確的結論是 ．（填入正確結論的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
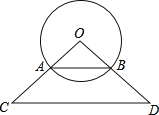
【題目】已知⊙O的半徑為12cm，弦AB=12
cm．
(1)求圓心O到弦AB的距離．
(2)若弦AB恰好是△OCD的中位線，以CD中點E為圓點，R為半徑作⊙E，當⊙O和⊙E相切時，求R的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
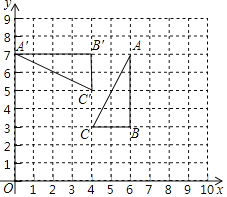
【題目】如圖，在平面直角坐標系中，△ABC和△A'B'C'的頂點都在格點上．
（1）將△ABC繞點B順時針旋轉90°后得到△A1BC1；
（2）若△A'B'C'是由△ABC繞某一點旋轉某一角度得到，則旋轉中心的坐標是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點A、B在數軸上分別表示數a，b．若A、B兩點間的距離記為d，則d和a，b之間的數量關系是d=|a-b|.
(1)數軸上有理數x與有理數－2所對應兩點之間的距離可以表示為______；
(2)|x+6|可以表示數軸上有理數x與有理數_______所對應的兩點之間的距離；
若|x+6|= |x -2|，則x=______；
(3)若a=1，b=-2，將數軸折疊，使得A點與﹣7表示的點重合，則B點與數______表示的點P重合；
(4)若數軸上M、N兩點之間的距離為11(M在N的左側)，且M、N兩點經過(3)中折疊后互相重合，則M、N兩點表示的數分別是：M：_____， N：_______；
(5)在題(3)的條件下，點A為定點，點B、P為動點，若移動點B、P中一點后，能否使相鄰兩點間距離相等？若能，請寫出移動方案.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，甲、乙、丙、丁、戊五名同學有以下說法：甲說：“直線BC不過點A”；乙說：“點A在直線CD外”； 丙說：“D在線段CB的反向延長線上；”丁說：“A，B，C，D兩兩連結，有5條線段” ； 戊說：“射線AD與射線CD不相交”． 其中說明正確的有（ ）．
A. 3人B. 4人C. 5人D. 2人
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在學習完《有理數》后，小奇對運算產生了濃厚的興趣．借助有理數的運算，定義了一種新運算“⊕”，規則如下：a⊕b＝a×b+2×a．
（1）求2⊕（﹣1）的值；
（2）求﹣3⊕（﹣4⊕
）的值；
（3）試用學習有理數的經驗和方法來探究這種新運算“⊕”是否具有交換律？請寫出你的探究過程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點A是拋物線
與x軸正半軸的交點，點B在拋物線上，其橫坐標為2，直線AB與y軸交于點
點M、P在線段AC上
不含端點
，點Q在拋物線上，且MQ平行于x軸，PQ平行于y軸
設點P橫坐標為m．
（1）求直線AB所對應的函數表達式．
（2）用含m的代數式表示線段PQ的長．
（3）以PQ、QM為鄰邊作矩形PQMN，求矩形PQMN的周長為9時m的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
