
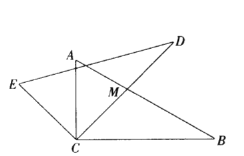
【題目】如圖,已知在![]() 中,
中,![]() ,將
,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,
,![]() 交直線
交直線![]() 于
于![]() .發現:
.發現:![]() .
.
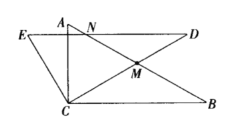
探究①:若![]() 恰好是
恰好是![]() 的中點,
的中點,![]() 交
交![]() 于
于![]() ,如圖2,求
,如圖2,求![]() 的長;
的長;
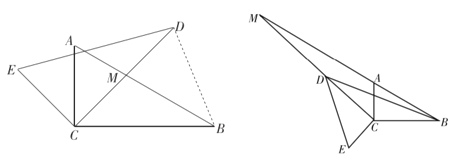
探究②:在旋轉過程中,當![]() 是等腰三角形時,求點
是等腰三角形時,求點![]() 所旋轉的路徑長(保留
所旋轉的路徑長(保留![]() )
)
【答案】發現:1;探究①:![]() ;探究②:
;探究②:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
發現:根據直角三角形中30度所對的直角邊等于斜邊的一半可得答案;
探究①:根據直角三角形斜邊上中線的性質可得![]() ,
,![]() ,結合
,結合![]() 可得
可得![]() ,然后根據
,然后根據![]() 進行計算;
進行計算;
探究②:分![]() 時和
時和![]() 時兩種情況,在每種情況下再分
時兩種情況,在每種情況下再分![]() 時和
時和![]() 時兩種情況,分別根據旋轉的性質和等腰三角形的性質求出旋轉角α,再根據弧長公式計算即可.
時兩種情況,分別根據旋轉的性質和等腰三角形的性質求出旋轉角α,再根據弧長公式計算即可.
解:發現:由題意得![]() ;
;
探究①:∵![]() ,M是斜邊
,M是斜邊![]() 的中點,
的中點,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
探究②:若![]() 時,連接
時,連接![]() ,由題意得
,由題意得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴當![]() 時,有
時,有![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴點![]() 所旋轉的路徑長為:
所旋轉的路徑長為:![]() ;
;
當![]() 時,有
時,有![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴點![]() 所旋轉的路徑長為:
所旋轉的路徑長為:![]() ;
;
若![]() 時,
時,
∵![]() ,
,
∵當![]() 時,有
時,有![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴點![]() 所旋轉的路徑長為:
所旋轉的路徑長為:![]() ,
,
同理,當![]() 時,有
時,有![]() ,
,
∴點![]() 所旋轉的路徑長為:
所旋轉的路徑長為:![]() ,
,
綜上所述,點![]() 所旋轉的路徑長為:
所旋轉的路徑長為:![]() 或
或![]() 或
或![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】為了解某市初中學生課外閱讀情況,調查小組對該市這學期初中學生閱讀課外書籍的冊數進行了抽樣調查,并根據調查結果繪制成如下統計圖.
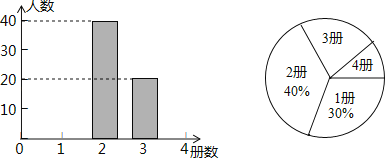
根據統計圖提供的信息,解答下列問題:
(1)本次抽樣調查的樣本容量是 ;
(2)補全條形統計圖;
(3)該市共有12000名初中生,估計該市初中學生這學期課外閱讀超過2冊的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
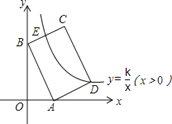
【題目】如圖,在平面直角坐標系中,矩形ABCD的邊AB:BC=3:2,點A(3,0),B(0,6)分別在x軸,y軸上,反比例函數y=![]() (x>0)的圖象經過點D,且與邊BC交于點E,則點E的坐標為__.
(x>0)的圖象經過點D,且與邊BC交于點E,則點E的坐標為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
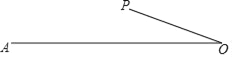
【題目】如圖,線段OA=2,OP=1,將線段OP繞點O任意旋轉時,線段AP的長度也隨之改變,則下列結論:
①AP的最小值是1,最大值是4;
②當AP=2時,△APO是等腰三角形;
③當AP=1時,△APO是等腰三角形;
④當AP=![]() 時,△APO是直角三角形;
時,△APO是直角三角形;
⑤當AP=![]() 時,△APO是直角三角形.
時,△APO是直角三角形.
其中正確的是( )
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為初三學生定制校服,對部分學生的服裝型號做了調查,結果如下:
型號 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列說法正確的是( )
A.男生服裝型號的眾數大于女生服裝型號的眾數
B.男生服裝型號的中位數等于女生服裝型號的中位數
C.男生服裝型號的眾數小于女生服裝型號的眾數
D.男生服裝型號的中位數大于女生服裝型號的中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
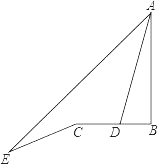
【題目】重慶朝天門碼頭位于置慶市油中半島的嘉陵江與長江交匯處,是重慶最古老的碼頭.如圖,小王在碼頭某點E處測得朝天門廣場上的某高樓AB的頂端A的仰角為45°,接著他沿著坡度為1:2.4的斜坡EC走了26米到達坡頂C處,到C處后繼續朝高樓AB的方向前行16米到D處,在D處測得A的仰角為74°,則此時小王距高樓的距離BD的為( )米(結果精確到1米,參考數據:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
A.12B.13C.15D.16
查看答案和解析>>
科目:初中數學 來源: 題型:
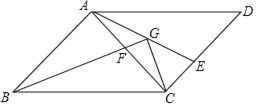
【題目】在平行四邊形ABCD中,∠ABC=45°,AB=AC,點E,F分別CD、AC邊上的點,且AF=CE,BF的延長線交AE于點G.
(1)若DE=2![]() ,AD=8,求AE.
,AD=8,求AE.
(2)若G是AE的中點,連接CG,求證:![]() AE+CG=BG.
AE+CG=BG.
查看答案和解析>>
科目:初中數學 來源: 題型:
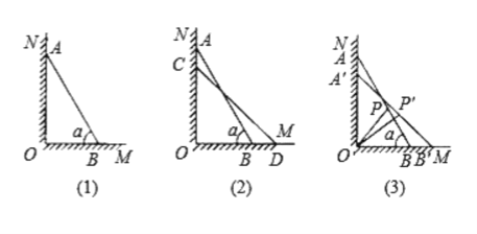
【題目】如圖(1)所示,一架長![]() 米的梯子
米的梯子![]() 斜靠在與地面
斜靠在與地面![]() 垂直的墻壁
垂直的墻壁![]() 上,梯子與地面所成的角
上,梯子與地面所成的角![]() 為
為![]() 度.
度.
(1)求圖(1)中的![]() 與
與![]() 的長度;
的長度;
(2)若梯子頂端![]() 沿
沿![]() 下滑,同時底端
下滑,同時底端![]() 沿
沿![]() 向右滑行.
向右滑行.
①如圖(2)所示,設![]() 點下滑到
點下滑到![]() 點,
點,![]() 點向右滑行到
點向右滑行到![]() 點,并且
點,并且![]() ,請計算
,請計算![]() 的長度;
的長度;
②如圖(3)所示,當![]() 點下滑到
點下滑到![]() ,
,![]() 點向右滑行到
點向右滑行到![]() 點時,梯子
點時,梯子![]() 的中點
的中點![]() 也隨之運動到
也隨之運動到![]() 點,若
點,若![]() ,試求
,試求![]() 的長度.
的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com