
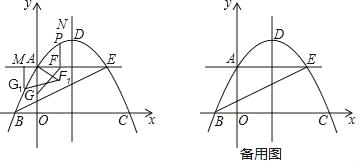
【題目】如圖,頂點為D的拋物線y=﹣![]() x2+
x2+![]() x+4與y軸交于點A,與x軸交于兩點B、C(點B在點C的左邊),點A與點E關于拋物線的對稱軸對稱,點B、E在直線y=kx+b(k,b為常數)上.
x+4與y軸交于點A,與x軸交于兩點B、C(點B在點C的左邊),點A與點E關于拋物線的對稱軸對稱,點B、E在直線y=kx+b(k,b為常數)上.
(1)求k,b的值;
(2)點P為直線AE上方拋物線上的任意一點,過點P作AE的垂線交AE于點F,點G為y軸上任意一點,當△PBE的面積最大時,求PF+FG+![]() OG的最小值;
OG的最小值;
(3)在(2)中,當PF+FG+![]() OG取得最小值時,將△AFG繞點A按順時方向旋轉30°后得到△AF1G1,過點G1作AE的垂線與AE交于點M.點D向上平移
OG取得最小值時,將△AFG繞點A按順時方向旋轉30°后得到△AF1G1,過點G1作AE的垂線與AE交于點M.點D向上平移![]() 個單位長度后能與點N重合,點Q為直線DN上任意一點,在平面直角坐標系中是否存在一點S,使以S、Q、M、N為頂點且MN為邊的四邊形為菱形?若存在,直接寫出點S的坐標;若不存在,請說明理由.
個單位長度后能與點N重合,點Q為直線DN上任意一點,在平面直角坐標系中是否存在一點S,使以S、Q、M、N為頂點且MN為邊的四邊形為菱形?若存在,直接寫出點S的坐標;若不存在,請說明理由.
【答案】(1)k=![]() ,b=1;(2)PF+FG+
,b=1;(2)PF+FG+![]() OG的最小值2+3
OG的最小值2+3![]() ;(3)存在,點S的坐標為:(﹣1,﹣1),(﹣1,9),(7,4).
;(3)存在,點S的坐標為:(﹣1,﹣1),(﹣1,9),(7,4).
【解析】
(1)由題意得:A(0,4)、B(-2,0)、D(3,![]() )、C(8,0)、E(6,4),則:過BE的直線為:y=
)、C(8,0)、E(6,4),則:過BE的直線為:y=![]() x+1;
x+1;
(2)設:P橫坐標為m,則P(m,-![]() m2+
m2+![]() +4),H(m,
+4),H(m,![]() m+1),則:PH=-
m+1),則:PH=-![]() m2+
m2+![]() +4-(
+4-(![]() m+1)=-
m+1)=-![]() (x-2)2+4,當x=2時,PH取得最大值,此時△PEB的面積也取得最大值;構造與y軸夾角為45度的直線OR,如圖所示,過點G作OR的垂線交OR于點R,則:RG=
(x-2)2+4,當x=2時,PH取得最大值,此時△PEB的面積也取得最大值;構造與y軸夾角為45度的直線OR,如圖所示,過點G作OR的垂線交OR于點R,則:RG=![]() ,則:PF+FG+
,則:PF+FG+![]() OG=PF+FG+GR,當F、G、R三點共線時,FG+GR有最小值,即可求解;
OG=PF+FG+GR,當F、G、R三點共線時,FG+GR有最小值,即可求解;
(3)存在.當四邊形為菱形,分在MNQ1S1的位置時、在MNQ2S2的位置時、在MNQ3S3的位置時三種情況分別求解.
(1)由題意得:A(0,4)、B(﹣2,0)、D(3,![]() )、C(8,0)、E(6,4),
)、C(8,0)、E(6,4),
則:過BE的直線為:y=![]() x+1;
x+1;
(2)延長PF交BE于點H,
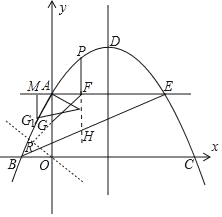
設:P橫坐標為m,則P(m,﹣![]() m2+
m2+![]() +4),H(m,
+4),H(m,![]() m+1),
m+1),
則:PH=﹣![]() m2+
m2+![]() +4﹣(
+4﹣(![]() m+1)=﹣
m+1)=﹣![]() (x﹣2)2+4,
(x﹣2)2+4,
當x=2時,PH取得最大值,此時△PEB的面積也取得最大值,
此時,P(2,6)、F(2,4),PF=2,
構造與y軸夾角為45度的直線OR,如圖所示,過點G作OR的垂線交OR于點R,
則:RG=![]() ,∴PF+FG+
,∴PF+FG+![]() OG=PF+FG+GR,
OG=PF+FG+GR,
當F、G、R三點共線時,FG+GR有最小值,
在Rt△AGF中,AF=AG=2,則:GF=2![]() ,
,
在Rt△ROG中,RO=RG,OG=2,則:RG=![]() ,
,
FG+GR=2![]() +
+![]() =3
=3![]() ,
,
故:PF+FG+![]() OG的最小值2+3
OG的最小值2+3![]() ;
;
(3)存在.如圖所示:
△AFG繞點A按順時方向旋轉30°后得到△AF1G1,
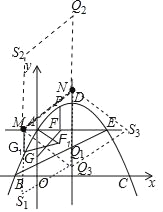
在Rt△G1AM中,AG1=2,∠AG1M=30°,
則:AM=1,∴M(﹣1,4),
點D向上平移![]() 個單位長度后能與點N重合,則:N(3,7),
個單位長度后能與點N重合,則:N(3,7),
則:MN=![]() =5,
=5,
當四邊形為菱形,在MNQ1S1的位置時,MS1=MN=5,則點S1(﹣1,﹣1),
當四邊形為菱形,在MNQ2S2的位置時,MS2=MN=5,則點S2(﹣1,9),
當四邊形為菱形,在MNQ3S3的位置時,點S3與點M關于對稱軸對稱,則點S3(7,4),
故:所求點S的坐標為:(﹣1,﹣1),(﹣1,9),(7,4).


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
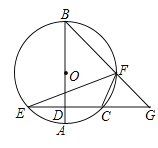
【題目】如圖,AB為⊙O的直徑,C,F為⊙O上兩點,過C作CD⊥AB于點D,交⊙O于點E,延長EC交BF的延長線于點G,連接CF,EG.
(1)求證:∠BFE=∠CFG;
(2)若FG=4,BF=6,CF=3.求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,拋物線y=ax2+bx+c與坐標軸分別交于點A(0,6),B(6,0),C(﹣2,0),點P是線段AB上方拋物線上的一個動點.
(1)求拋物線的解析式;
(2)當點P運動到什么位置時,△PAB的面積有最大值?
(3)過點P作x軸的垂線,交線段AB于點D,再過點P做PE∥x軸交拋物線于點E,連結DE,請問是否存在點P使△PDE為等腰直角三角形?若存在,求出點P的坐標;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只箱子里共有3個球,其中2個白球,1個紅球,它們除顏色外均相同。
(1)從箱子中任意摸出一個球是白球的概率是多少?
(2)從箱子中任意摸出一個球,不將它放回箱子,攪勻后再摸出一個球,求兩次摸出球的都是白球的概率,并畫出樹狀圖。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點M(4,0),以點M為圓心、2為半徑的圓與x軸交于點A、B.已知拋物線![]() 過點A和B,與y軸交于點C.
過點A和B,與y軸交于點C.
(1)求點C的坐標,并畫出拋物線的大致圖象.
(2)點Q(8,m)在拋物線![]() 上,點P為此拋物線對稱軸上一個動點,求PQ+PB的最小值.
上,點P為此拋物線對稱軸上一個動點,求PQ+PB的最小值.
(3)CE是過點C的⊙M的切線,點E是切點,求OE所在直線的解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀一段文字,再回答下列問題:已知在平面內兩點的坐標為![]() ,
,![]() ,則該兩點間距離公式為
,則該兩點間距離公式為![]() .同時,當兩點在同一坐標軸上或所在直線平行于
.同時,當兩點在同一坐標軸上或所在直線平行于![]() 軸、平行于
軸、平行于![]() 軸時,兩點間的距離公式可化簡成
軸時,兩點間的距離公式可化簡成![]() 與
與![]() .
.
(1)若已知兩點![]() ,
,![]() ,試求
,試求![]() 兩點間的距離;
兩點間的距離;
(2)已知點![]() 在平行于
在平行于![]() 軸的直線上,點
軸的直線上,點![]() 的縱坐標為7,點
的縱坐標為7,點![]() 的縱坐標為
的縱坐標為![]() ,試求
,試求![]() 兩點間的距離;
兩點間的距離;
(3)已知一個三角形各頂點的坐標為![]() ,
,![]() ,
,![]() ,你能判定這三點是否共線?若共線請說明理由,若不共線請求出圖形的面積.
,你能判定這三點是否共線?若共線請說明理由,若不共線請求出圖形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的兩條角平分線BD、CE交于O,且∠A=60°,則下列結論中不正確的是( )
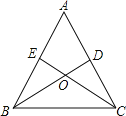
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC,AB的垂直平分線交線段AC于D,若△ABC和△DBC的周長分別是60 cm和38 cm,則△ABC的腰長和底邊BC的長分別是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,以△ABC的一邊BC為直徑的⊙O分別交AB、AC于D、E,下面判斷中:①當△ABC為等邊三角形時,△ODE是等邊三角形;②當△ODE是等邊三角形,△ABC為等邊三角形;③當∠A=45°時,△ODE是直角三角形;④當△ODE是直角三角形時,∠A=45°.正確的結論有( )
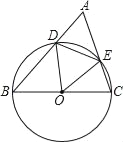
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com