
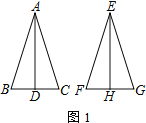
【題目】如圖1,AB=AC,EF=EG,△ABC≌△EFG,AD⊥BC于點D,EH⊥FG于點H
(1) 直接寫出AD、EH的數量關系:___________________
(2) 將△EFG沿EH剪開,讓點E和點C重合
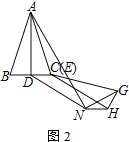
① 按圖2放置△EHG,將線段CD沿EH平移至HN,連接AN、GN,求證:AN⊥GN
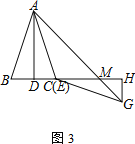
② 按圖3放置△EHG,B、C(E)、H三點共線,連接AG交EH于點M.若BD=1,AD=3,求CM的長度
【答案】(1)AD=EH;(2)見解析;(3)CM=2.
【解析】
(1)由△ABC≌△EFG,可知面積相等,利用面積公式可得高相等;
(2)如圖所示,設AN、CH交于點P,CH、NG交于點O,由CD平移到NH可知四邊形CDNH為平行四邊形,所以CH=DN=AD,可得出△AND為等腰三角形,再由GH=CD=NH可得出△GHN為等腰三角形,由于兩個等腰三角形頂角相等,可推出底角相等,在△OPN和△OGH中,可由∠OPN=∠PND=∠NGH,可推出∠PNO=90°,則AN⊥GN;
(3由AD⊥BH,GH⊥BH,可得AD∥GH,所以![]() ,再由DH=DC+EH=1+3=4,
,再由DH=DC+EH=1+3=4,
可求出DM=3,∴CM=3-1=2.
解:(1)∵△ABC≌△EFG,
∴BC=FG,![]()
∴![]()
∴AD=EH
(2)如圖所示,設AN、CH交于點P,CH、NG交于點O

CD平移到NH可得四邊形CDNH為平行四邊形
∴CH=DN,∠CDN=∠CHN,DN∥CH
又∵EH=AD,∴AD=DN,即△AND為等腰三角形
∵GH=CD=NH,∴△GHN為等腰三角形,
∵∠ADN=∠ADC+∠CDN=90°+∠CDN
∠NHG=∠CHG+∠CHN=90°+∠CHN
而∠CDN=∠CHN
∴∠ADN=∠NHG,
∴![]() ,
,![]()
∴∠AND=∠NGH
又∵DN∥CH,∴∠AND=∠NPH,∴∠NGH=∠NPH
在△OPN和△OGH中
∠NPH=∠NGH,∠PON=∠GOH,
∴∠PNO=∠OGH=90°,
∴AN⊥GN
(3)由△ABC≌△EFG可得CD=BD=1,EH=AD=3
∵AD⊥BH,GH⊥BH
∴AD∥GH,∴![]() ,∴
,∴![]()
又∵DH=DC+EH=1+3=4
∴DM=3,
∴CM=DM-DC=3-1=2.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
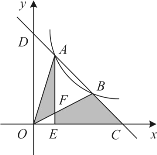
【題目】如圖,一次函數 y=-x+b 與反比例函數y=![]() (x>0)的圖象交于 A,B 兩點,與 x 軸、y軸分別交于C,D 兩點,連接 OA,OB,過 A 作 AE⊥x 軸于點 E,交 OB 于點F,設點 A 的橫坐標為 m. 若 S△OAF+S 四邊形 EFBC=4,則 m 的值是( )
(x>0)的圖象交于 A,B 兩點,與 x 軸、y軸分別交于C,D 兩點,連接 OA,OB,過 A 作 AE⊥x 軸于點 E,交 OB 于點F,設點 A 的橫坐標為 m. 若 S△OAF+S 四邊形 EFBC=4,則 m 的值是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分12分)
已知:把Rt△ABC和Rt△DEF按如圖(1)擺放(點C與點E重合),點B、C(E)、F在同一條直線上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如圖(2),△DEF從圖(1)的位置出發,以1 cm/s的速度沿CB向△ABC勻速移動,在△DEF移動的同時,點P從△ABC的頂點B出發,以2 cm/s的速度沿BA向點A勻速移動.當△DEF的頂點D移動到AC邊上時,△DEF停止移動,點P也隨之停止移動.DE與AC相交于點Q,連接PQ,設移動時間為t(s)(0<t<4.5).

解答下列問題:
(1)當t為何值時,點A在線段PQ的垂直平分線上?
(2)連接PE,設四邊形APEC的面積為y(cm2),求y與t之間的函數關系式;是否存在某一時刻t,使面積y最小?若存在,求出y的最小值;若不存在,說明理由.
(3)是否存在某一時刻t,使P、Q、F三點在同一條直線上?若存在,求出此時t的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
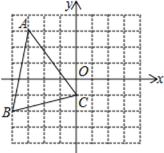
【題目】如圖,在下列帶有坐標系的網格中,△ABC的頂點都在邊長為1的小正方形的頂點上
(1) 直接寫出坐標:A__________,B__________
(2) 畫出△ABC關于y軸的對稱的△DEC(點D與點A對應)
(3) 用無刻度的直尺,運用全等的知識作出△ABC的高線BF(保留作圖痕跡)
查看答案和解析>>
科目:初中數學 來源: 題型:
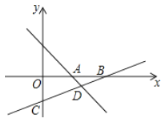
【題目】如圖,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,直線
,直線![]() 經過點
經過點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,與直線
,與直線![]() 相交于點
相交于點![]() .
.
![]() 求直線
求直線![]() 的函數關系式;
的函數關系式;
![]() 點
點![]() 是
是![]() 上的一點,若
上的一點,若![]() 的面積等于
的面積等于![]() 的面積的
的面積的![]() 倍,求點
倍,求點![]() 的坐標.
的坐標.
![]() 設點
設點![]() 的坐標為
的坐標為![]() ,是否存在
,是否存在![]() 的值使得
的值使得![]() 最小?若存在,請求出點
最小?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC和△ECD都是等邊三角形

(1)如圖1,若B、C、D三點在一條直線上,求證:BE=AD;
(2)保持△ABC不動,將△ECD繞點C順時針旋轉,使∠ACE=90°(如圖2),BC與DE有怎樣的位置關系?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com