
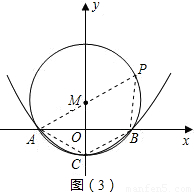
 所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
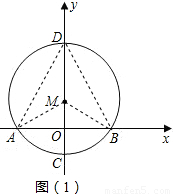 解:(1)如圖(1),
解:(1)如圖(1), MB=1,
MB=1,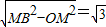 ,
,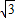 ,0).(5分)
,0).(5分) .
. x2-1.(6分)
x2-1.(6分) AB•OC+
AB•OC+ AB•OD
AB•OD AB•CD
AB•CD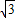 cm2.(9分)
cm2.(9分)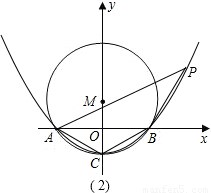
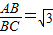 ,
,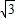 ,PA=
,PA=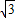 PB=6.(10分)
PB=6.(10分)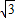 -
-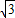 =2
=2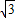 ,y=PA•sin30°=3.(11分)
,y=PA•sin30°=3.(11分)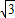 ,3)的坐標滿足y=
,3)的坐標滿足y= x2-1,
x2-1, x2-1上,存在點P(2
x2-1上,存在點P(2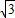 ,3),
,3),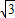 ,3)也符合題意.
,3)也符合題意.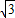 ,3)或(-2
,3)或(-2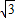 ,3).(12分)
,3).(12分)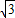 ,3),(-2
,3),(-2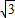 ,3),無最后一步不扣分.下面的方法相同.
,3),無最后一步不扣分.下面的方法相同.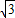 ,0),M(0,1)代入,
,0),M(0,1)代入,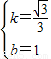 ,
,
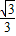 x+1.(10分)
x+1.(10分)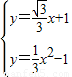 ,
,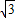 ,3).(11分)
,3).(11分)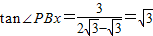 ,
, x2-1上,存在點(2
x2-1上,存在點(2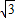 ,3),使△ABC∽△PAB.
,3),使△ABC∽△PAB.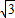 ,3)也符合題意.
,3)也符合題意.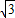 ,3)或(-2
,3)或(-2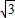 ,3).(12分)
,3).(12分)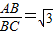 ,
,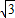 ,PA=
,PA=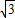 AB=6.(10分)
AB=6.(10分)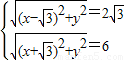 ,
,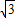 ,3).(11分)
,3).(11分)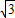 ,3)的坐標滿足y=
,3)的坐標滿足y= x2-1,
x2-1, x2-1上,存在點P(2
x2-1上,存在點P(2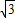 ,3),使△ABC∽△PAB.
,3),使△ABC∽△PAB.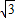 ,3)也符合題意.
,3)也符合題意.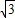 ,3)或(-2
,3)或(-2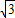 ,3).(12分)
,3).(12分)

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2009-2010學年九年級(下)數學綜合測試卷(解析版) 題型:解答題
 所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
查看答案和解析>>
科目:初中數學 來源:第27章《二次函數》中考題集(46):27.3 實踐與探索(解析版) 題型:解答題
 所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》中考題集(48):2.8 二次函數的應用(解析版) 題型:解答題
 所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
查看答案和解析>>
科目:初中數學 來源:第20章《二次函數和反比例函數》中考題集(43):20.5 二次函數的一些應用(解析版) 題型:解答題
 所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
查看答案和解析>>
科目:初中數學 來源:2006年甘肅省酒泉市中考數學試卷(課標卷)(解析版) 題型:解答題
 所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
所對的圓心角為120°,已知圓的半徑為2cm,并建立如圖所示的直角坐標系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com