
 ,D為斜邊BC上的一點(D與B、C均不重合
,D為斜邊BC上的一點(D與B、C均不重合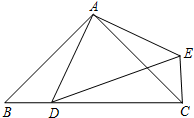 ),連接AD,把△ABD繞點A按逆時針旋轉后得到△ACE,連接DE,設BD=x.
),連接AD,把△ABD繞點A按逆時針旋轉后得到△ACE,連接DE,設BD=x.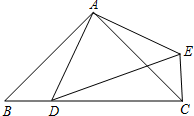
 ,
,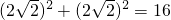 ,
, DC•CE=
DC•CE= (4-x)x.
(4-x)x. (4-x)x=1.5,
(4-x)x=1.5, (4-x)x(0<x<4),
(4-x)x(0<x<4), (x-2)2+2,
(x-2)2+2, <0,
<0,

 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:初中數學 來源: 題型:
 如圖,△ABC是等腰直角三角形,BC是斜邊,點P是△ABC內一定點,延長BP至P′,將△ABP繞點A旋轉后,與△ACP′重合,如果AP=
如圖,△ABC是等腰直角三角形,BC是斜邊,點P是△ABC內一定點,延長BP至P′,將△ABP繞點A旋轉后,與△ACP′重合,如果AP=| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC繞點A按順時針方向旋轉45°后得到△AB′C′,若AB=2,則線段BC在上述旋轉過程中所掃過部分(陰影部分)的面積是
如圖,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC繞點A按順時針方向旋轉45°后得到△AB′C′,若AB=2,則線段BC在上述旋轉過程中所掃過部分(陰影部分)的面積是查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•資陽)如圖,△ABC是等腰三角形,點D是底邊BC上異于BC中點的一個點,∠ADE=∠DAC,DE=AC.運用這個圖(不添加輔助線)可以說明下列哪一個命題是假命題?( )
(2012•資陽)如圖,△ABC是等腰三角形,點D是底邊BC上異于BC中點的一個點,∠ADE=∠DAC,DE=AC.運用這個圖(不添加輔助線)可以說明下列哪一個命題是假命題?( )查看答案和解析>>
科目:初中數學 來源: 題型:
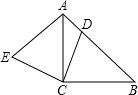 已知:如圖,△ABC是等腰直角三角形,D為斜邊AB上任意一點(不與A,B重合),連接CD,作EC⊥DC,且EC=DC,連接AE.
已知:如圖,△ABC是等腰直角三角形,D為斜邊AB上任意一點(不與A,B重合),連接CD,作EC⊥DC,且EC=DC,連接AE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com