

 =1,則 A(1,0)、B(3,0).
=1,則 A(1,0)、B(3,0).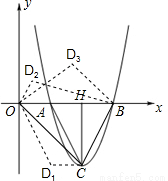 (2)假設存在符合條件的D點.
(2)假設存在符合條件的D點. ;tan∠HBC=2,BC=
;tan∠HBC=2,BC= .
.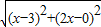 =
=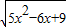 ,
,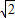 =
=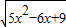 ,解得:x=
,解得:x= ,x=1(舍)
,x=1(舍) ,
, ).
).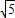 ,得:
,得: ,
, )、(2,1).
)、(2,1). .
. ).
).

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 已知二次函數的圖象是經過點A(1,0),B(3,0),E(0,6)三點的一條拋物線.
已知二次函數的圖象是經過點A(1,0),B(3,0),E(0,6)三點的一條拋物線.查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
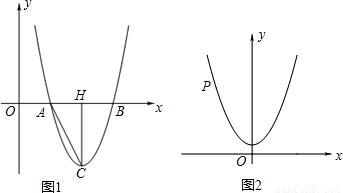
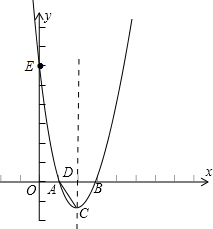
 閱讀材料:如圖1,過△ABC的三個頂點分別作出與水平線垂直的三條直線,外側兩條直線之間的距離叫△ABC的“水平寬”(a),中間的這條直線在△ABC內部線段的長度叫△ABC的“鉛垂高”(h).我們可得出一種計算三角形面積的新方法:S△ABC=
閱讀材料:如圖1,過△ABC的三個頂點分別作出與水平線垂直的三條直線,外側兩條直線之間的距離叫△ABC的“水平寬”(a),中間的這條直線在△ABC內部線段的長度叫△ABC的“鉛垂高”(h).我們可得出一種計算三角形面積的新方法:S△ABC=| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,將拋物線y=-
如圖,將拋物線y=-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com