
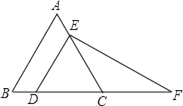
【題目】如圖,△ABC是等邊三角形,點D、E分別在邊BC、AC上,AE=BD,連接DE,過點E作EF⊥DE,交線段BC的延長線于點F.
(1)求證:CE=CF;
(2)若BD=![]() CE,AB=9,求線段DF的長.
CE,AB=9,求線段DF的長.
【答案】(1)證明見解析;(2)12.
【解析】
(1)由題意可證△DEC是等邊三角形,可求∠ECD=∠DEC=60°,根據三角形外角等于不相鄰的兩個內角的和,可求∠CEF=∠CFE=30°,即可得CE=CF;
(2)由題意可得BD=3,CD=6,即可求DF的長.
(1)∵△ABC是等邊三角形
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°
∵AE=BD
∴AC﹣AE=BC﹣BD
∴CE=CD,且∠ACB=60°
∴△CDE是等邊三角形
∴∠ECD=∠DEC=60°
∵EF⊥DE
∴∠DEF=90°
∴∠CEF=30°
∵∠DCE=∠CEF+∠CFE=60°
∴∠CEF=∠CFE=30°
∴CE=CF
(2)∵BD=![]() CE,CE=CD
CE,CE=CD
∴BD=![]() CD
CD
∵AB=9
∴BC=9
∴BD=3,CD=6
∵CE=CF=CD
∴CF=6
∴DF=DC+CF=12


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,借助直角三角板可以找到一元二次方程的實數根,比如對于方程 ![]() ,操作步驟是:
,操作步驟是:
第一步:根據方程系數特征,確定一對固定點A(0,1),B(5,2);
第二步:在坐標平面中移動一個直角三角板,使一條直角邊恒過點A,另一條直角邊恒過點B;
第三步:在移動過程中,當三角板的直角頂點落在x軸上點C處時,點C 的橫坐標m即為該方程的一個實數根(如圖1)
第四步:調整三角板直角頂點的位置,當它落在x軸上另一點D處時,點D 的橫坐標為n即為該方程的另一個實數根。

(1)在圖2 中,按照“第四步“的操作方法作出點D(請保留作出點D時直角三角板兩條直角邊的痕跡)
(2)結合圖1,請證明“第三步”操作得到的m就是方程 ![]() 的一個實數根;
的一個實數根;
(3)上述操作的關鍵是確定兩個固定點的位置,若要以此方法找到一元二次方程 ![]() 的實數根,請你直接寫出一對固定點的坐標;
的實數根,請你直接寫出一對固定點的坐標;
(4)實際上,(3)中的固定點有無數對,一般地,當 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 與a,b,c之間滿足怎樣的關系時,點P(
與a,b,c之間滿足怎樣的關系時,點P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一對固定點?
)就是符合要求的一對固定點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,2條直線 最多有![]() =1個交點,3條直線最多有
=1個交點,3條直線最多有![]() =3個交點,4條直線最多有
=3個交點,4條直線最多有![]() =6個交點,……由此猜想,8條直線最多有___個交點.
=6個交點,……由此猜想,8條直線最多有___個交點.

A. 32 B. 16 C. 28 D. 40
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮與小明做投骰子(質地均勻的正方體)的實驗與游戲.
(1)在實驗中他們共做了50次試驗,試驗結果如下:
朝上的點數 | 1 | 2 | 3 | 4 | 5 | 6 |
出現的次數 | 10 | 9 | 6 | 9 | 8 | 8 |
①填空:此次實驗中,“1點朝上”的頻率是 ;
(2)在游戲時兩人約定:每次同時擲兩枚骰子,如果兩枚骰子的點數之和超過6,則小亮獲勝,否則小明獲勝.則小亮與小明誰獲勝的可能性大?試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
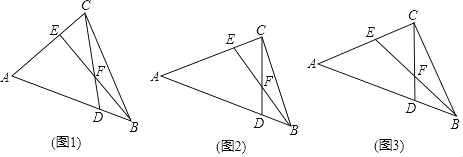
【題目】如圖,在△ABC中,點D在邊AB上,點E在邊AC上,CE=BD,連接CD,BE,BE與CD相交于點F.
(1)如圖1,若△ACD為等邊三角形,且CE=DF,求∠CEF的度數;
(2)如圖2,若AC=AD,求證:EF=FB;
(3)如圖3,在(2)的條件下,若∠CFE=45°,△BCD的面積為4,求線段CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一內部裝有水的直圓柱形水桶,桶高20公分;另有一直圓柱形的實心鐵柱,柱高30公分,直立放置于水桶底面上,水桶內的水面高度為12公分,且水桶與鐵柱的底面半徑比為2:1.今小賢將鐵柱移至水桶外部,過程中水桶內的水量未改變,若不計水桶厚度,則水桶內的水面高度變為多少公分?( )
A.4.5
B.6
C.8
D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y=ax2+bx的圖象過點A(﹣1,3),頂點B的橫坐標為1.
(1)求這個二次函數的表達式;
(2)點P在該二次函數的圖象上,點Q在x軸上,若以A、B、P、Q為頂點的四邊形是平行四邊形,求點P的坐標;
(3)如圖3,一次函數y=kx(k>0)的圖象與該二次函數的圖象交于O、C兩點,點T為該二次函數圖象上位于直線OC下方的動點,過點T作直線TM⊥OC,垂足為點M,且M在線段OC上(不與O、C重合),過點T作直線TN∥y軸交OC于點N.若在點T運動的過程中, ![]() 為常數,試確定k的值.
為常數,試確定k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸交于點A、B,與y軸交于點C,過點C作CD∥x軸,與拋物線交于點D,若OA=1,CD=4,則線段AB的長為( ) 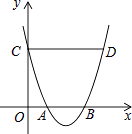
A.2
B.1
C.3
D.1.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com