
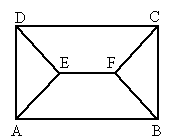
如圖所示,矩形ABCD中,AB>AD,∠DAB與∠ADC的平分線交于E點,∠ABC與∠BCD的平分線交于F點.試問EF與AB、BC有怎樣的關系,并說明理由.
|
解: EF=AB-BC.證明如下:如圖所示,延長 AE交DC于M,延長CF交AB于N點.
因為四邊形 ABCD是矩形,所以∠ DAB=∠ADC=90°,AD=BC ,AB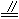 DC. DC.
因為 DE平分∠ADC,AE平分∠DAB,所以, 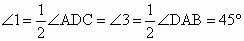 , ,
所以∠ DEA=90°=∠DEM,所以∠ 3=∠4(三角形內角和等于180°),所以 AD=DM同理NB=BC,所以DM=NB,所以 E為AM中點(等腰三角形頂角平分線是底邊中線).同理 F是NC中點,所以 DC-DM=AB-NVB,即MC=AN.因為 M、N分別在DC、AB上,所以 MC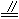 AN,所以四邊形MANC是平行四邊形, AN,所以四邊形MANC是平行四邊形,
所以 AM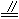 CN,所以AE CN,所以AE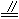 NF,所以四邊形EANF為平行四邊形, NF,所以四邊形EANF為平行四邊形,
所以 EF=AN=AB-NB=AB-BC. |


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
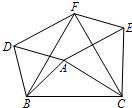 18、如圖所示,在△ABC中,分別以AB、AC、BC為邊在BC的同側作等邊△ABD,等邊△ACE、等邊△BCF.
18、如圖所示,在△ABC中,分別以AB、AC、BC為邊在BC的同側作等邊△ABD,等邊△ACE、等邊△BCF.查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
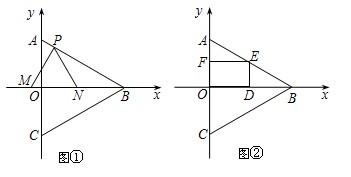
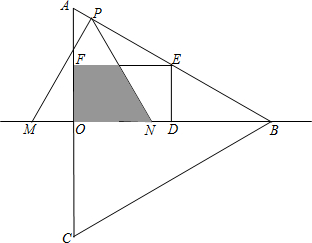 邊在△AOB內部作如圖所示的矩形ODEF,點E在線段AB上.
邊在△AOB內部作如圖所示的矩形ODEF,點E在線段AB上.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•邵陽)如圖所示,在△ABC中,AB=AC,∠A<90°,邊BC、CA、AB的中點分別是D、E、F,則四邊形AFDE是( )
(2012•邵陽)如圖所示,在△ABC中,AB=AC,∠A<90°,邊BC、CA、AB的中點分別是D、E、F,則四邊形AFDE是( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com