
【題目】甲開汽車,乙騎自行車從M地出發沿一條公路勻速前往N地,乙先出發一段時間后甲才出發,設乙行駛的時間為t(h),甲乙兩人之間的距離為y(km),y與t的函數關系如圖1所示,其中點C的坐標為(![]() ,
,![]() ),請解決以下問題:
),請解決以下問題:
(1)甲比乙晚出發幾小時?
(2)分別求出甲、乙二人的速度;
(3)丙騎摩托車與乙同時出發,從N地沿同一條公路勻速前往M地,若丙經過![]() h與乙相遇.
h與乙相遇.
①設丙與M地的距離為S(km),行駛的時間為t(h),求S與t之間的函數關系式(不用寫自變量的取值范圍)
②丙與乙相遇后再用多少時間與甲相遇.

【答案】(1)1h;(2) 乙的速度為20km/h,甲的速度為60 km/h;(3)①S=﹣40t+80,②丙與乙相遇后再用![]() 與甲相遇
與甲相遇
【解析】
試題(1)根據圖象即可直接作出判斷;
(2)根據OA段和AB段時間的關系可求得甲、乙速度之間的關系,然后根據BC段,兩人所走的路程的差是![]() km,所用的時間已知,即可列方程求解;
km,所用的時間已知,即可列方程求解;
(3)①利用待定系數法即可求得函數的解析式;②利用甲和丙的路程與時間之間的關系式組成方程組,求得甲、丙相遇的時間,則相遇的時間即可求得.
試題解析:(1)1 h;
(2)由圖1可知甲、乙在乙出發1.5小時后相遇,

因為甲比乙晚出發1小時,
所以甲僅用0.5小時走了乙用1.5小時所用的路程,
所以甲的速度是乙的速度的3倍.
設乙的速度為xkm/h,
則甲的速度為3xkm/h,由圖1得:(3x﹣x)(![]() ﹣1.5)=
﹣1.5)=![]() ;
;
解得:x=20,
所以乙的速度為20km/h,甲的速度為60 km/h,
(3)①設s=kt+b.當t=![]() 時,s=
時,s=![]() x20=
x20=![]() ;
;
當t=0時,S=20×4=80;代入得k=﹣40,b=80
故丙距M地的路程S與時間t的函數關系式為S=﹣40t+80.
②由甲的速度為60 km/h且比乙晚出發一小時易得S甲=60t﹣60,與S丙=﹣40t+80,
聯立![]() ,
,
解得t=![]() ,即在丙出發
,即在丙出發![]() 小時后,甲、丙相遇.
小時后,甲、丙相遇.
∵![]() -
-![]() =
=![]() ,
,
∴丙與乙相遇后再用![]() 與甲相遇.
與甲相遇.


科目:初中數學 來源: 題型:
【題目】等腰三角形ABC在平面直角坐標系中的位置如圖所示,已知點A(﹣6,0),點B在原點,CA=CB=5,把等腰三角形ABC沿x軸正半軸作無滑動順時針翻轉,第一次翻轉到位置①,第二次翻轉到位置②…依此規律,第15次翻轉后點C的橫坐標是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校在八年級開設了數學史、詩詞賞析、陶藝三門校本課程,若小波和小睿兩名同學每人隨機選擇其中一門課程,則小波和小睿選到同一課程的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學生在素質教育基地進行社會實踐活動,幫助農民伯伯采摘了黃瓜和茄子共40kg,了解到這些蔬菜的種植成本共42元,還了解到如下信息: 
(1)請問采摘的黃瓜和茄子各多少千克?
(2)這些采摘的黃瓜和茄子可賺多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+(a+3)x+3(a≠0)與x軸交于點A(4,0),與y軸交于點B,在x軸上有一動點E(m,0)(0<m<4),過點E作x軸的垂線交直線AB于點N,交拋物線于點P,過點P作PM⊥AB于點M.
(1)求a的值和直線AB的函數表達式;
(2)設△PMN的周長為C1 , △AEN的周長為C2 , 若 ![]() =
= ![]() ,求m的值;
,求m的值;
(3)如圖2,在(2)條件下,將線段OE繞點O逆時針旋轉得到OE′,旋轉角為α(0°<α<90°),連接E′A、E′B,求E′A+ ![]() E′B的最小值.
E′B的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,直線l1經過(2,3)和(﹣1,﹣3),直線l2經過原點O,且與直線l1交于點P(﹣2,a).
(1)求a的值;
(2)(﹣2,a)可看成怎樣的二元一次方程組的解?
(3)設直線l1與y軸交于點A,你能求出△APO的面積嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,把△ABC繞AB邊上的點D順時針旋轉90°得到△A′B′C′,A′C′交AB于點E,若AD=BE,則△A′DE的面積是 . 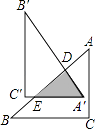
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了檢驗教室里的矩形門框是否合格,某班的四個學習小組用三角板和細繩分別測得如下結果,其中不能判定門框是否合格的是( )
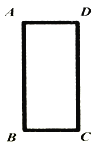
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com