有一種等腰三角形,經過它的一個頂點的一條直線把這個等腰三角形分成了兩個小三角形,這兩個小三角形也是等腰三角形,則這種等腰三角形的頂角度數是 (至少要寫出兩種情況)
【答案】
分析:本題要利用三角形內角和定理求解.由于本題中經過等腰三角形頂點的直線沒有明確是經過頂角的頂點還是底角的頂點,因此本題要分情況討論.
解答:解:設該等腰三角形的底角是x;
①當過頂角的頂點的直線把它分成了兩個等腰三角形,則AC=BC,AD=CD=BD,
設∠A=x°,
則∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°,
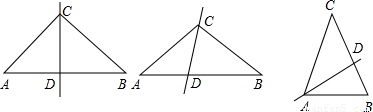
∴x+x+x+x=180,
解得x=45,
則頂角是90°;
②如圖,AC=BC=BD,AD=CD,
設∠B=x°,
∵AC=BC,
∴∠A=∠B=x°,
∵AD=CD,
∴∠ACD=∠A=x°,
∴∠BDC=∠A+∠ACD=2x°,
∵BC=BD,
∴∠BCD=∠BDC=2x°,
∴∠ACB=3x°,
∴x+x+3x=180,x=36°,則頂角是108°.
③當過底角的角平分線把它分成了兩個等腰三角形,則有AC=BC,AB=AD=CD,
設∠C=x°,
∵AD=CD,
∴∠CAD=∠C=x°,
∴∠ADB=∠CAD+∠C=2x°,
∵AD=AB,
∴∠B=∠ADB=2x°,
∵AC=BC,
∴∠CAB=∠B=2x°,
∵∠CAB+∠B+∠C=180°,
∴x+2x+2x=180,
x=36°,
則頂角是36°.
④當∠A=x°,∠ABC=∠ACB=3x°時,也符合,如圖
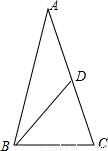
AD=BD,BC=DC,
∠A=∠ABD=x,∠DBC=∠BDC=2x,
則x+3x+3x=180°,
x=
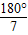
因此等腰三角形頂角的度數為36°或90°或108°或
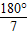
.
點評:本題考查了等腰三角形的性質及其判定.作此題的時候,首先大致畫出符合條件的圖形,然后根據等腰三角形的性質、三角形的內角和定理及其推論找到角之間的關系,列方程求解.



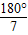
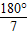 .
.
