
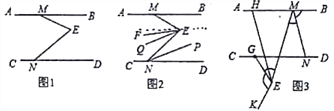
【題目】已知:直線AB∥CD,點M,N分別在直線AB,CD上,點E為平面內一點.
(1)如圖1,∠BME,∠E,∠END的數量關系為 (直接寫出答案);
(2)如圖2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度數(用用含m的式子表示)
(3)如圖3,點G為CD上一點,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于點H,探究∠GEK,∠BMN,∠GEH之間的數量關系(用含n的式子表示)
【答案】(1)∠E=∠BME+∠END;(2)![]() m°;(3)∠GEK=∠BMN+n·∠GEH
m°;(3)∠GEK=∠BMN+n·∠GEH
【解析】試題分析:(1)過點E作l∥AB,利用平行線的性質可得∠1=∠BME,∠2=∠DNE,由∠MEN=∠1+∠2,等量代換可得結論;(2)利用角平分線的性質可得∠NEF=![]() ∠MEN,∠ENP=
∠MEN,∠ENP=![]() ∠END,由EQ∥NP,可得∠QEN=∠ENP=
∠END,由EQ∥NP,可得∠QEN=∠ENP=![]() ∠END,由(1)的結論可得∠MEN=∠BME+∠END,等量代換得出結論;(3)由已知可得∠EMN=
∠END,由(1)的結論可得∠MEN=∠BME+∠END,等量代換得出結論;(3)由已知可得∠EMN=![]() ∠BMN,∠GEM=
∠BMN,∠GEM=![]() ∠GEK,由EH∥MN,可得∠HEM=∠ENM=
∠GEK,由EH∥MN,可得∠HEM=∠ENM=![]() ∠BMN,因為∠GEH=∠GEM-∠HEM,等量代換得出結論.
∠BMN,因為∠GEH=∠GEM-∠HEM,等量代換得出結論.
試題解析:
(1)如圖1,過點E作l∥AB,
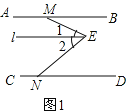
∵AB∥CD,
∴l∥AB∥CD,
∴∠1=∠BME,∠2=∠DNE,
∵∠MEN=∠1+∠2,
∴∠E=∠BME+∠END,
故答案為:∠E=∠BME+∠END;
(2)如圖2,
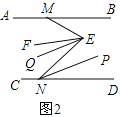
∵EF平分∠MEN,NP平分∠END,
∴∠NEF=![]() ∠MEN,∠ENP=
∠MEN,∠ENP=![]() ∠END,
∠END,
∵EQ∥NP,
∴∠QEN=∠ENP=![]() ∠END,
∠END,
∵∠MEN=∠BME+∠END,
∴∠MEN-∠END=∠BME=m°,
∴∠FEQ=∠NEF-∠NEQ=![]() ∠MEN
∠MEN![]() ∠END=
∠END=![]() (∠MEN∠END)=
(∠MEN∠END)= ![]() m°;
m°;
(3)∠GEK=∠BMN+n∠GEH.
如圖3,
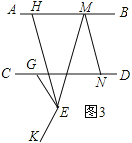
∵∠BMN=n∠EMN,∠GEK=n∠GEK,
∴∠EMN=![]() ∠BMN,∠GEM=
∠BMN,∠GEM=![]() ∠GEK,
∠GEK,
∵EH∥MN,
∴∠HEM=∠ENM=![]() ∠BMN,
∠BMN,
∵∠GEH=∠GEM-∠HEM=![]() ∠GEK
∠GEK![]() ∠BMN,
∠BMN,
∴n∠GEH=∠GEK-∠BMN,
即∠GEK=∠BMN+n∠GEH.


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,點E為AD的中點,延長CE交BA的延長線于點F.
(1)求證:AB=AF;
(2)若BC=2AB,∠BCD=100°,求∠ABE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某籃球隊對隊員進行定點投籃測試,每人每天投籃10次,現對甲、乙兩名隊員在五天中進球數(單位:個)進行統計,結果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
經過計算,甲進球的平均數為8,方差為3.2.
(1)求乙進球的平均數和方差;
(2)如果綜合考慮平均成績和成績穩定性兩方面的因素,從甲、乙兩名隊員中選出一人去參加定點投籃比賽,應選誰?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
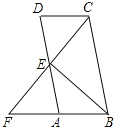
【題目】如圖①,△ABC與△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且點D在AB邊上,AB、EF的中點均為O,連結BF、CD、CO,顯然點C、F、O在同一條直線上,可以證明△BOF≌△COD,則BF=CD.
解決問題
(1)將圖①中的Rt△DEF繞點O旋轉得到圖②,猜想此時線段BF與CD的數量關系,并證明你的結論;
(2)如圖③,若△ABC與△DEF都是等邊三角形,AB、EF的中點均為O,上述(1)中的結論仍然成立嗎?如果成立,請說明理由;如不成立,請求出BF與CD之間的數量關系;
(3)如圖④,若△ABC與△DEF都是等腰三角形,AB、EF的中點均為0,且頂角∠ACB=∠EDF=α,請直接寫出![]() 的值(用含α的式子表示出來)
的值(用含α的式子表示出來)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠加工一批零件,為了提高工人工作積極性,工廠規定每名工人每天薪金如下:生產的零件不超過a件,則每件3元,超過a件,超過部分每件b元,如圖是一名工人一天獲得薪金y(元)與其生產的件數x(件)之間的函數關系式,則下列結論錯誤的( )
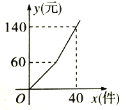
A.a=20
B.b=4
C.若工人甲一天獲得薪金180元,則他共生產45件.
D.人乙一天生產40(件),則他獲得薪金140元
查看答案和解析>>
科目:初中數學 來源: 題型:
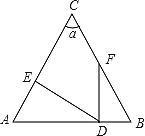
【題目】如圖∠A=∠B,∠C=![]() ,DE⊥AC于點E,FD⊥AB于點D.
,DE⊥AC于點E,FD⊥AB于點D.
(1)若∠EDA=25°,則∠EDF=________°;
(2)若∠A=65°,則∠EDF=_______°;
(3)若![]() =50°,則∠EDF=_______°;
=50°,則∠EDF=_______°;
(4)若∠EDF=65°,則![]() _______°;
_______°;
(5)∠EDF與![]() 的關系為_______.
的關系為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
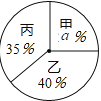
【題目】某校學生會決定從三名學生會干事中選拔一名干事,對甲、乙、丙三名候選人進行了筆試和面試,三人的測試成績如下表所示:
測試項目 | 測試成績/分 | ||
甲 | 乙 | 丙 | |
筆試 | 75 | 80 | 90 |
面試 | 93 | 70 | 68 |
根據錄用程序,學校組織200名學生采用投票推薦的方式,對三人進行民主測評,三人得票率(沒有棄權,每位同學只能推薦1人)如扇形統計圖所示,每得一票記1分.
(1)扇形統計圖中![]() = , 分別計算三人民主評議的得分;
= , 分別計算三人民主評議的得分;
(2)根據實際需要,學校將筆試、面試、民主評議三項得分按4:3:3的比例確定個人成績,得分最高者將被選中,通過計算說明三人中誰被選中?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某開發區計劃在一塊四邊形的空地ABCD上種植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,種植每平方米草皮的預算費用為300元,若第一年對草坪的保養費用占種植草皮總預算的4%,以后每年的保養費用都將在前一年的基礎上遞增2%,求第三年的草坪保養費用.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四幅圖象分別表示變量之間的關系,請按圖象的順序,將下面的四種情境與之對應排序.正確的順序是( )

①籃球運動員投籃時,投出去的籃球的高度與時間的關系;
②去超市購買同一單價的水果,所付費用與水果數量的關系;
③李老師使用的是一種含月租的手機計費方式,則他每月所付話費與通話時間的關系;
④周末,小明從家到圖書館,看了一段時間書后,按原速度原路返回,小明離家的距離與時間的關系
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com