【題目】已知三角形兩邊的長分別是4和10，則此三角形第三邊的長不可能是（ ）
A.6
B.7
C.9.5
D.10
科目：初中數學 來源： 題型：
【題目】 如圖，一次函數y=x+3的圖象與x軸，y軸交于A，B兩點，與反比例函數
的圖象相交于C，D兩點，分別過C，D兩點作y軸，x軸的垂線，垂足為E，F，連接CF，DE．有下列四個結論：
①△CEF與△DEF的面積相等；②△AOB∽△FOE；③△DCE≌△CDF；④AC=BD．
其中正確的結論是（ ）
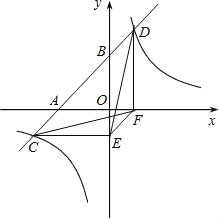
A．①② B．①②③
C．①②③④ D．②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】九年級（1）班的全體同學根據自己的興趣愛好參加了六個學生社團（每個學生必須參加且只參加一個），為了了解學生參加社團的情況，學生會對該班參加各個社團的人數進行了統計，繪制成了如圖不完整的扇形統計圖，已知參加“讀書社”的學生有10人，請解答下列問題：
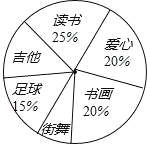
（1）該班的學生共有 名；該班參加“愛心社”的人數為 名，若該班參加“吉他社”與“街舞社”的人數相同，則“吉他社”對應扇形的圓心角的度數為 ；
（2）一班學生甲、乙、丙是“愛心社”的優秀社員，現要從這三名學生中隨機選兩名學生參加“社區義工”活動，請你用畫樹狀圖或列表的方法求出恰好選中甲和乙的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，∠ABC，∠BCD的平分線BE，CF分別與AD相交于點E、F，BE與CF相交于點G，若AB=3，BC=5，CF=2，則BE的長為（ ）
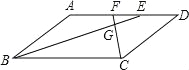
A．2
B．4 C．4 D．5
查看答案和解析>>
科目：初中數學 來源： 題型：
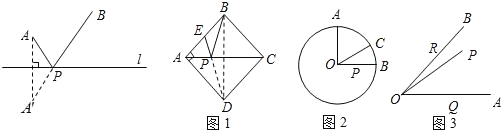
【題目】幾何模型：
條件：如圖，A、B是直線l同旁的兩個定點．
問題：在直線l上確定一點P，使PA+PB的值最小．
方法：作點A關于直線l的對稱點A′，連結A′B交l于點P，則PA+PB=A′B的值最小（不必證明）．
模型應用：
（1）如圖1，正方形ABCD的邊長為2，E為AB的中點，P是AC上一動點．連結BD，由正方形對稱性可知，B與D關于直線AC對稱．連結ED交AC于P，則PB+PE的最小值是 ；
（2）如圖2，⊙O的半徑為2，點A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一動點，求PA+PC的最小值；
（3）如圖3，∠AOB=45°，P是∠AOB內一點，PO=10，Q、R分別是OA、OB上的動點，求△PQR周長的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
