
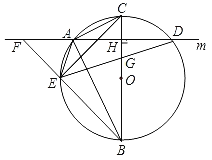
【題目】如圖,在⊙O的內接△ABC中,∠CAB=90°,AB=2AC,過點A作BC的垂線m交⊙O于另一點D,垂足為H,點E為![]() 上異于A,B的一個動點,射線BE交直線m于點F,連接AE,連接DE交BC于點G.
上異于A,B的一個動點,射線BE交直線m于點F,連接AE,連接DE交BC于點G.
(1)求證:△FED∽△AEB;
(2)若![]() =
=![]() ,AC=2,連接CE,求AE的長;
,AC=2,連接CE,求AE的長;
(3)在點E運動過程中,若BG=![]() CG,求tan∠CBF的值.
CG,求tan∠CBF的值.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據同角的余角重疊得出∠EAB=∠ECB,然后根據三角形相似的判定定理判定即可得出結論;
(2)根據相交弦定理得出DH=AH=![]() ,再根據勾股定理得,BH=
,再根據勾股定理得,BH=![]() ,進而求出BE=CE=
,進而求出BE=CE=![]() ,進而求出EF=
,進而求出EF=![]() ,FD=
,FD=![]() ,借助(1)的結論即可得出結論;
,借助(1)的結論即可得出結論;
(3)根據平行線分線段成比例得出判![]() ,根據平行線的性質得出tan∠CBF=tan∠CGT=
,根據平行線的性質得出tan∠CBF=tan∠CGT=![]() ,根據圓周角定理得出tan∠CED=tan∠ABC,進而得出
,根據圓周角定理得出tan∠CED=tan∠ABC,進而得出![]() ,再結合已知條件
,再結合已知條件![]() ,即可得出結論.
,即可得出結論.
解:(1)∵⊙O的內接△ABC中,∠CAB=90°,
∴BC是⊙O的直徑,
∵點E為![]() 上異于A,B的一個動點,
上異于A,B的一個動點,
∴∠CEB=90°,
∴∠ECB+∠EBC=90°,
∵過點A作BC的垂線m交⊙O于另一點D,垂足為H,
∴∠FHB=90°,
∴∠FBH+∠HFB=90°,
∴∠HFB=∠ECB,
∵∠EAB=∠ECB,
∴∠EAB=∠HFB,
∵∠FBA=∠ADE,
∴△FED∽△AEB;
(2)∵∠CAB=90°,AB=2AC,AC=2,
∴AB=4,
根據勾股定理得,BC=2![]() ,
,
∵AD⊥BC,BC是⊙O的切線,
∴DH=AH=![]() =
=![]() =
=![]() ,
,
在Rt△AHB中,根據勾股定理得,BH=![]() =
=![]() ,
,
∵![]() ,BC是⊙O的直徑,
,BC是⊙O的直徑,
∴BE=CE,∠ECB=∠EBC=45°,
∵BC=2![]() ,∠BEC=90°,
,∠BEC=90°,
∴BE=CE=![]() ,
,
∵∠FHB=90°,∠EBC=45°,BH=![]() ,
,
∴FH=BH=![]() ,BF=
,BF=![]() ,
,
∴EF=BF﹣BE=![]() ,FD=FH+DH=
,FD=FH+DH=![]() ,
,
∵△FED∽△AEB,
∴![]() ,
,
∴ ,
,
∴AE=![]() ;
;
(3)如圖,過點G作GT⊥CE于T,

∵∠CEB=90°,
∴TG∥EB,
∴![]() ,∠CGT=∠CBF,
,∠CGT=∠CBF,
∴tan∠CBF=tan∠CGT=![]() ,
,
∵![]() ,
,
∴∠CED=∠ABC,
∴tan∠CED=tan∠ABC,
∴![]() ,
,
∵![]() ,BG=
,BG=![]() CG,
CG,
∴ET=![]() CT,
CT,![]() ,
,
∴![]() ,
,
∴tan∠CBF=tan∠CGT=![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
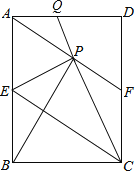
【題目】如圖,在矩形ABCD中,E是AB邊的中點,沿EC對折矩形ABCD,使B點落在點P處,折痕為EC,連結AP并延長AP交CD于F點,連結CP并延長CP交AD于Q點.給出以下結論:
①四邊形AECF為平行四邊形;
②∠PBA=∠APQ;
③△FPC為等腰三角形;
④△APB≌△EPC.
其中正確結論的個數為( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
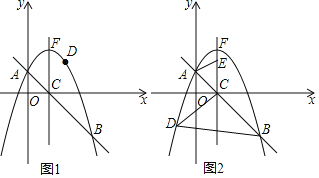
【題目】如圖,在平面直角坐標系xOy中,將拋物線y=﹣x2+bx+c與直線y=﹣x+1相交于點A(0,1)和點B(3,﹣2),交x軸于點C,頂點為點F,點D是該拋物線上一點.
(1)求拋物線的函數表達式;
(2)如圖1,若點D在直線AB上方的拋物線上,求△DAB的面積最大時點D的坐標;
(3)如圖2,若點D在對稱軸左側的拋物線上,且點E(1,t)是射線CF上一點,當以C、B、D為頂點的三角形與△CAE相似時,求所有滿足條件的t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出:如何將一個長為17,寬為1的長方形經過剪一剪,拼一拼,形成一個正方形.(下列所有圖中每個小方格的邊長都為1,剪拼過程中材料均無剩余)
問題探究:我們從長為5,寬為1的長方形入手.
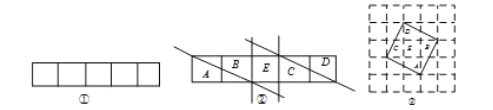
(1)如圖①是一個長為5,寬為1的長方形.把這個長方形剪一剪、拼一拼后形成正方形,則正方形的面積應為_____________,設正方形的邊長為![]() ,則
,則![]() _________;
_________;
(2)我們可以把有些帶根號的無理數的被開方數表示成兩個正整數平方和的形式,比如![]() .類比此,可以將(1)中的
.類比此,可以將(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的幾何意義可以理解為:以長度2和3為直角邊的直角三角形的斜邊長為
的幾何意義可以理解為:以長度2和3為直角邊的直角三角形的斜邊長為![]() ;類比此,(2)中的
;類比此,(2)中的![]() 可以理解為以長度________和__________為直角邊的直角三角形斜邊的長;
可以理解為以長度________和__________為直角邊的直角三角形斜邊的長;
(4)剪一剪:由(3)可畫出如圖②的分割線,把長方形分成![]() 五部分;
五部分;
(5)拼一拼:把圖②中五部分拼接得到如圖③的正方形;
問題解決:仿照上面的探究方法請把圖④中長為17,寬為1的長方形剪一剪,在圖⑤中畫出拼成的正方形.(說明:圖④的分割過程不作評分要求,只對圖⑤中畫出的最終結果評分)
![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的頂點D關于射線CP的對稱點G落在正方形內,連接BG并延長交邊AD于點E,交射線CP于點F.連接DF,AF,CG.
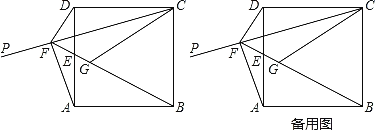
(1)試判斷DF與BF的位置關系,并說明理由;
(2)若CF=4![]() ,DF=2,求AE的長;
,DF=2,求AE的長;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以AC為直徑的⊙O與AB邊交于點D,點E是邊BC的中點.

(1)、求證:BC 2=BDBA;
(2)、判斷DE與⊙O位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(模型介紹)
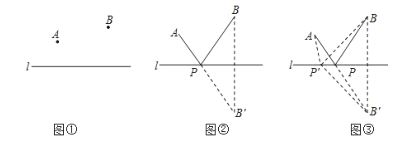
古希臘有一個著名的“將軍飲馬問題”,大致內容如下:古希臘一位將軍,每天都要巡查河岸同側的兩個軍營![]() .他總是先去
.他總是先去![]() 營,再到河邊飲馬,之后,再巡查
營,再到河邊飲馬,之后,再巡查![]() 營.如圖①,他時常想,怎么走才能使每天走的路程之和最短呢?大數學家海倫曾用軸對稱的方法巧妙地解決了這個問題.如圖②,作點
營.如圖①,他時常想,怎么走才能使每天走的路程之和最短呢?大數學家海倫曾用軸對稱的方法巧妙地解決了這個問題.如圖②,作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連結
,連結![]() 與直線
與直線![]() 交于點
交于點![]() ,連接
,連接![]() ,則
,則![]() 的和最小.請你在下列的閱讀、理解、應用的過程中,完成解答.理由:如圖③,在直線
的和最小.請你在下列的閱讀、理解、應用的過程中,完成解答.理由:如圖③,在直線![]() 上另取任一點
上另取任一點![]() ,連結
,連結![]() ,
,![]() ,
,![]() ,∵直線
,∵直線![]() 是點
是點![]() ,
,![]() 的對稱軸,點
的對稱軸,點![]() ,
,![]() 在
在![]() 上,
上,
(1)∴![]() __________,
__________,![]() _________,∴
_________,∴![]() ____________.在
____________.在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,即
,即![]() 最小.
最小.
(歸納總結)
在解決上述問題的過程中,我們利用軸對稱變換,把點![]() 在直線同側的問題轉化為在直線的兩側,從而可利用“兩點之間線段最短”,即轉化為“三角形兩邊之和大于第三邊”的問題加以解決(其中點
在直線同側的問題轉化為在直線的兩側,從而可利用“兩點之間線段最短”,即轉化為“三角形兩邊之和大于第三邊”的問題加以解決(其中點![]() 為
為![]() 與
與![]() 的交點,即
的交點,即![]() ,
,![]() ,
,![]() 三點共線).由此,可拓展為“求定直線上一動點與直線同側兩定點的距離和的最小值”問題的數學模型.
三點共線).由此,可拓展為“求定直線上一動點與直線同側兩定點的距離和的最小值”問題的數學模型.
(模型應用)
(2)如圖④,正方形![]() 的邊長為4,
的邊長為4,![]() 為
為![]() 的中點,
的中點,![]() 是
是![]() 上一動點.求
上一動點.求![]() 的最小值.
的最小值.
解析:解決這個問題,可借助上面的模型,由正方形對稱性可知,點![]() 與
與![]() 關于直線
關于直線![]() 對稱,連結
對稱,連結![]() 交
交![]() 于點
于點![]() ,則
,則![]() 的最小值就是線段
的最小值就是線段![]() 的長度,則
的長度,則![]() 的最小值是__________.
的最小值是__________.

(3)如圖⑤,圓柱形玻璃杯,高為![]() ,底面周長為
,底面周長為![]() ,在杯內離杯底
,在杯內離杯底![]() 的點
的點![]() 處有一滴蜂蜜,此時一只螞蟻正好在外壁,離杯上沿
處有一滴蜂蜜,此時一只螞蟻正好在外壁,離杯上沿![]() 與蜂蜜相對的點
與蜂蜜相對的點![]() 處,則螞蟻到達蜂的最短路程為_________
處,則螞蟻到達蜂的最短路程為_________![]() .
.

(4)如圖⑥,在邊長為2的菱形![]() 中,
中,![]() ,將
,將![]() 沿射線
沿射線![]() 的方向平移,得到
的方向平移,得到![]() ,分別連接
,分別連接![]() ,
,![]() ,
,![]() ,則
,則![]() 的最小值為____________.
的最小值為____________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com