【題目】某超市用5 000元購進一批新品種的蘋果進行試銷，由于銷售狀況良好，超市又調撥11 000元資金購進該品種蘋果，但這次的進貨價比試銷時每千克多了0.5元，購進蘋果數量是試銷時的2倍．
（1）試銷時該品種蘋果的進貨價是每千克多少元？
（2）如果超市將該品種蘋果按每千克7元的定價出售，當大部分蘋果售出后，余下的蘋果定價為4元，超市在這兩次蘋果銷售中的盈利不低于4 100元，那么余下的蘋果最多多少千克？
【答案】（1）5元（2）300千克
【解析】
試題（1）設試銷時該品種蘋果的進貨價是每千克x元，則實際進貨價為（0.5+x）元，根據這次購進蘋果數量是試銷時的2倍，列方程求解；
（2）設余下的蘋果為y千克，求出總購進的蘋果數量，根據超市在這兩次蘋果銷售中的盈利不低于4 100元，列不等式求解．
試題解析：
（1）設試銷時該品種蘋果的進貨價是每千克x元，則實際進貨價為（0.5+x）元，
由題意得，
，
解得：x=5，
經檢驗，x=5是原分式方程的解，且符合題意，
答：試銷時該品種蘋果的進貨價是每千克5元；
（2）由（1）得，總共購進蘋果：5000÷5×3=3000（kg），
設余下的蘋果為y千克，
由題意得，7+4y﹣5000﹣11000≥4 100，
解得：y≤300．
答：余下的蘋果最多為300千克．
星級口算天天練系列答案
芒果教輔達標測試卷系列答案科目：初中數學 來源： 題型：
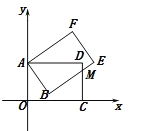
【題目】將兩個全等的矩形AOCD和矩形ABEF放置在如圖所示的平面直角坐標系中，已知A(0，5)，邊BE交邊CD于M，且ME=2，CM=4．
（1）求AD的長；
（2）求經過A、B、D三點的拋物線解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，A（1，0），B（4，0），M（5，3）．動點P從點A出發，沿x軸以每秒1個單位長的速度向右移動，且過點P的直線l：y=-x+b也隨之移動．設移動時間為t秒．
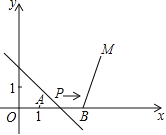
（1）當t=1時，求l的解析式；
（2）若l與線段BM有公共點，確定t的取值范圍；
（3）直接寫出t為何值時，點M關于l的對稱點落在y軸上．如不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
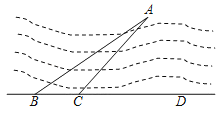
【題目】如圖，為測量小島A到公路BD的距離，先在點B處測得∠ABD＝37°，再沿BD方向前進150m到達點C，測得∠ACD＝45°，求小島A到公路BD的距離．(參考數據：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某初中學生為了解該校學生喜歡球類活動的情況，隨機抽取了若干名學生進行問卷調查（要求每位學生只能填寫一種自己喜歡的球類），并將調査的結果繪制成如下的兩幅不完整的統計圖．
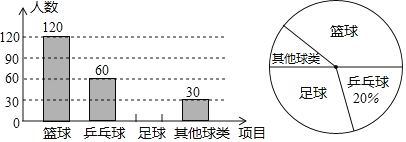
請根據圖中提供的信息，解答下面的問題
（1）參加調査的學生共有 人，在扇形圖中，表示“其他球類”的扇形圓心角為 度；
（2）將條形圖補充完整；
（3）若該校有2300名學生，則估計喜歡“足球”的學生共有 人．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC是等腰直角三角形，∠ACB＝90°，點A在反比例函數y＝﹣
的圖象上，點B、C都在反比例函數y＝﹣
的圖象上，AB∥x軸，則點A的坐標為（ ）
A.(﹣
，2
)B.(﹣
，)C.(﹣，)D.(﹣2，)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】長沙市為推進養老服務工作的深入開展，在科學規劃養老服務布局等方面作了大量工作，該市的養老機構擁有的養老床位數從2016年底的2萬個增長到2018年底的2．42萬個．
（1）求該市這兩年養老床位數的年平均增長率；
（2）該市青竹湖社區養老中心擬建造三類養老專用房間（提供一個床位的單人間、提供兩個床位的雙人間、提供三個床位的三人間）共100間，設單人間有
間（
），雙人間的數量是單人間的2倍，且三人間的數量不少于單人間和雙人間的數量之和，求此100間房建成后至少可提供床位多少個？
查看答案和解析>>
科目：初中數學 來源： 題型：
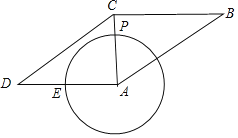
【題目】如圖，已知P是半徑為3的⊙A上一點，延長AP到點C，使AC＝4，以AC為對角線作ABCD，AB＝4
，⊙A交邊AD于點E，當ABCD面積為最大值時，
的長為（ ）
A.
πB.πC.
πD.3π
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
