久草视频播放,日韩在线二区,国产精品久久一区二区三区

精英家教網 > 初中數學 > 題目詳情

【題目】解下列方程組

（1）；

（2）；

（3）．

【答案】（1）；（2）；（3）

【解析】

（1）首先由方程①求出x的值，然后將x的值代入②中，即可求出y的值.

(2) 方程組利用代入消元法求出解即可；

(3) 根據代入消元法，化三元一次方程組為二元一次方程組，再根據加減消元法，可得一元一次方程，求出一元一次方程的解，再逐步代入，可得方程組的解．

解：（1）由①得：x＝2，

把x＝2代入②得：y＝5，

則方程組的解為；

（2），

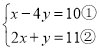①+②×4得：9x＝54，

解得：x＝6，

把x＝6代入②得：y＝﹣1，

則方程組的解為；

（3）把①代入②得：2x﹣3y+2（y+x）＝5，

整理得：4x﹣y＝5④，

把①代入③得：x+2y+y+x＝13，

整理得：2x+3y＝13⑤，

④×3+⑤得：14x＝28，

解得：x＝2，

把x＝2代入④得：y＝3，

把x＝2，y＝3代入①得：z＝5，

則方程組的解為．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】如圖1（注：與圖2完全相同），二次函數y= x2+bx+c的圖象與x軸交于A（3，0），B（﹣1，0）兩點，與y軸交于點C．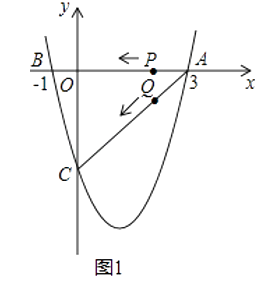

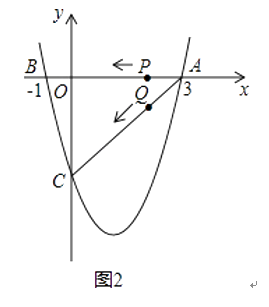
（1）求該二次函數的解析式；
（2）設該拋物線的頂點為D，求△ACD的面積（請在圖1中探索）；
（3）若點P，Q同時從A點出發，都以每秒1個單位長度的速度分別沿AB，AC邊運動，其中一點到達端點時，另一點也隨之停止運動，當P，Q運動到t秒時，△APQ沿PQ所在的直線翻折，點A恰好落在拋物線上E點處，請直接判定此時四邊形APEQ的形狀，并求出E點坐標（請在圖2中探索）．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，△ABC的頂點坐標分別為A（﹣6，0），B（4，0），C（0，8），把△ABC沿直線BC翻折，點A的對應點為D，拋物線y=ax2﹣10ax+c經過點C，頂點M在直線BC上．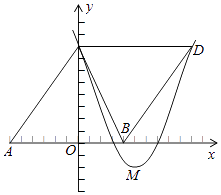

（1）證明四邊形ABCD是菱形，并求點D的坐標；
（2）求拋物線的對稱軸和函數表達式；
（3）在拋物線上是否存在點P，使得△PBD與△PCD的面積相等？若存在，直接寫出點P的坐標；若不存在，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，正方形ABCB1中，AB=1，AB與直線l的夾角為30°，延長CB1交直線l于點A1 ，作正方形A1B1C1B2 ，延長C1B2交直線l于點A2 ，作正方形A2B2C2B3 ，延長C2B3交直線l于點A3 ，作正方形A3B3C3B4 ， …，依此規律，則A2016A2017= ．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，AB∥CD，CF平分∠ECD，HC⊥CF交直線AB于H，AG平分∠HAE交HC于G，EJ∥AG交CF于J，∠AEC＝80°，則下列結論正確的有（　　）個．

①∠BAE+∠ECD＝80°；②CG平分∠ICE；③∠AGC＝140°；④∠EJC﹣∠AGH＝90°．

A.1B.2C.3D.4

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】等腰Rt△ACB，∠ACB＝90°，AC＝BC，點A、C分別在x軸、y軸的正半軸上．

（1）如圖1，求證：∠BCO＝∠CAO

（2）如圖2，若OA＝5，OC＝2，求B點的坐標

（3）如圖3，點C（0，3），Q、A兩點均在x軸上，且S△CQA＝18．分別以AC、CQ為腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM，連接MN交y軸于P點，OP的長度是否發生改變？若不變，求出OP的值；若變化，求OP的取值范圍．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，拋物線y=﹣ x2+bx+e與x軸交于點A（﹣3，0）、點B（9，0），與y軸交于點C，頂點為D，連接AD、DB，點P為線段AD上一動點．
（1）求拋物線的解析式；
（2）如圖1，過點P作BD的平行線，交AB于點Q，連接DQ，設AQ=m，△PDQ的面積為S，求S關于m的函數解析式，以及S的最大值；

（3）如圖2，拋物線對稱軸與x軸交與點G，E為OG的中點，F為點C關于DG對稱的對稱點，過點P分別作直線EF、DG的垂線，垂足為M、N，連接MN，直接寫出△PMN為等腰三角形時點P的坐標．