
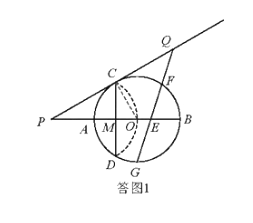
【題目】如圖,已知⊙O的半徑為2,AB為直徑,CD為弦,AB與CD交于點M,將弧CD沿著CD翻折后,點A與圓心O重合,延長OA至P,使AP=OA,鏈接PC。

(1)求CD的長;
(2)求證:PC是⊙O的切線;
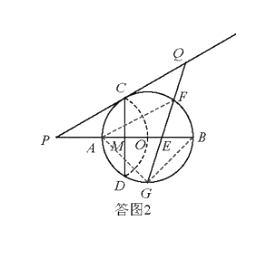
(3)點G為弧ADB的中點,在PC延長線上有一動點Q,連接QG交AB于點E,交弧BC于點F(F與B、C不重合)。問GEGF是否為定值?如果是,求出該定值;如果不是,請說明理由。
【答案】(1)2![]() ;(2)證明過程見解析;(3)定值為8.
;(2)證明過程見解析;(3)定值為8.
【解析】
試題分析:(1)連接OC,根據折疊圖形的性質得出OM=1,根據勾股定理的性質得出CD的長度;(2)首先根據勾股定理求出PC的長度,然后根據勾股定理的逆定理得出切線;(3)連接GA、AF、GB,根據題意得出△AGE與△FGA相似,從而得出GE·GF=![]() ,然后根據等腰直角三角形的性質得出答案.
,然后根據等腰直角三角形的性質得出答案.
試題解析:(1)如答圖1,連接OC ∵![]() 沿CD翻折后,A與O重合 ∴OM=
沿CD翻折后,A與O重合 ∴OM=![]() OA=1,CD⊥OA
OA=1,CD⊥OA
∵OC=2 ∴CD=2CM=2![]() =2
=2![]()
(2)∵PA=OA=2,AM=OM=1,CM=![]() 又∵
又∵![]() CMP=∠OMC=90° ∴PC=
CMP=∠OMC=90° ∴PC=![]() =2
=2![]()
∵OC=2,PO=4 ∴![]() ∴∠PCO=90° ∴PC與☉O相切
∴∠PCO=90° ∴PC與☉O相切
(3)GE·GF為定值,理由如下: 如答圖2,連接GA、AF、GB ∵G為![]() 中點 ∴
中點 ∴![]()
∴∠BAG=∠AFG ∵∠AGE=∠FGA ∴△AGE∽△FGA ∴![]()
∴GE·GF=![]() ∵AB為直徑,AB=4 ∴∠BAG=∠ABG=45° ∴AG=2
∵AB為直徑,AB=4 ∴∠BAG=∠ABG=45° ∴AG=2![]() ∴GE·GF=
∴GE·GF=![]() =8
=8


 學業測評一課一測系列答案
學業測評一課一測系列答案 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案科目:初中數學 來源: 題型:
【題目】某企業生產并銷售某種產品,假設銷售量與產量相等,如圖中的折線ABD、線段CD分別表示該產品每千克生產成本y1(單位:元)、銷售價y2(單位:元)與產量x(單位:kg)之間的函數關系.
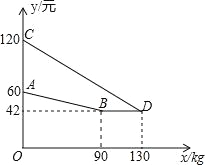
(1)求線段AB所表示的y1與x之間的函數表達式;線段CD所表示的y2與x之間的函數表達式.
(2)當該產品產量為多少時,獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,正確的個數有( )
①1的算術平方根是1;②(-1)2的算術平方根是-1;③一個數的算術平方根等于它本身,這個數只能是零;④-4沒有算術平方根.
A. 1個 B. 2個 C. 3個 D. 4個;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種糧大戶共有5塊小麥試驗地,每塊試驗地今年的收成與去年相比情況如下(增產為正,減產為負,單位:kg):49,-30,12,-15,28,請你計算一下,今年的小麥產量與去年相比增產________kg.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com