已知拋物線y=ax2+bx+c與拋物線y=-x2-3x+7的形狀相同,頂點在直線x=1上,且頂點到x軸的距離為5,則此拋物線的解析式為 .
【答案】
分析:先根據拋物線y=ax
2+bx+c與拋物線y=-x
2-3x+7的形狀相同可知a=±1,則拋物線解析式為y=±x
2+bx+c,由頂點在直線x=1上可求出b的值,再根據頂點到x軸的距離為5求出c的值即可.
解答:解:∵拋物線y=ax
2+bx+c與拋物線y=-x
2-3x+7的形狀相同,
∴a=±1,
∴拋物線解析式為y=±x
2+bx+c,
∵拋物線頂點在直線x=1上,
∴a=±1,
∴當a=-1時,-
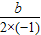
=1,
∴b=2;
當a=1時,-
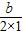
=1,
∴b=-2,
∴拋物線解析式為y=-x
2+2x+c=-(x-1)
2+c+1,或y=x
2-2x+c=(x-1)
2+c-1,
∵拋物線頂點到x軸的距離為5.
∴當y=x
2-2x+c=(x-1)
2+c-1
∴|c-1|=5,解得c=-4或c=6,
∴此時拋物線的解析式為:y=x
2-2x+6 或y=x
2-2x-4;
∵當拋物線的解析式為y=-x
2+2x+c=-(x-1)
2+c+1時,
∴|c+1|=5,解得c=4或c=-6,
∴此時拋物線的解析式為:y=-x
2+2x+4 或y=-x
2+2x-6.
∴拋物線的解析式為:y=x
2-2x+6或y=x
2-2x-4或y=-x
2+2x+4或y=-x
2+2x-6.
點評:本題考查的是二次函數的圖象與幾何變換,解答此題的關鍵是根據拋物線的對稱軸方程得出拋物線的頂點式,得出c的值,進而得出拋物線的解析式.

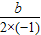 =1,
=1,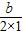 =1,
=1,

 與x軸的另一個交點為E.
與x軸的另一個交點為E. 如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=
如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=