
【題目】如圖,點 P 是∠AOB 內部一定點
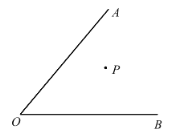
(1)若∠AOB=50°,作點 P 關于 OA 的對稱點 P1,作點 P 關于 OB 的對稱點 P2,連 OP1、OP2,則∠P1OP2=___.
(2)若∠AOB=α,點 C、D 分別在射線 OA、OB 上移動,當△PCD 的周長最小時,則∠CPD=___(用 α 的代數式表示).
【答案】100° 180°-2α
【解析】
(1)根據對稱性證明∠P1OP2=2∠AOB,即可解決問題;
(2)如圖,作點P關于OA的對稱點P1,作點P關于OB的對稱點P2,連P1P2交OA于C,交OB于D,連接PC,PD,此時△PCD的周長最小.利用(1)中結論,根據對稱性以及三角形內角和定理即可解決問題;
(1)如圖,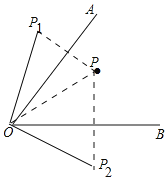
由對稱性可知:∠AOP=∠AOP1,∠POB=∠BOP2,
∴∠P1OP2=2∠AOB=100°,
故答案為100°.
(2)如圖,作點P關于OA的對稱點P1,作點P關于OB的對稱點P2,連P1P2交OA于C,交OB于D,連接PC,PD,此時△PCD的周長最小.
根據對稱性可知:∠OP1C=∠OPC,∠OP2D=∠OPD,∠P1OP2=2∠AOB=2α.
∴∠CPD=∠OP1C+∠OP2D=180°-2α.
故答案為180°-2α.


科目:初中數學 來源: 題型:
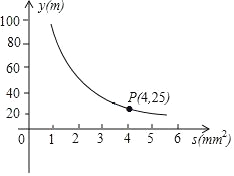
【題目】你吃過拉面嗎?實際上在做拉面的過程中就滲透著數學知識:一定體積的面團做成拉面,面條的總長度y(m)是面條的粗細(橫截面積)S(mm2)的反比例函數,其圖象如圖所示.
(1)寫出y(m)與S(mm2)的函數關系式;
(2)求當面條粗2mm2時,面條的總長度是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小山同學結合學習一次函數的經驗和自己的思考,按以下方式探究函數![]() 的圖象與性質,并嘗試解決相關問題.
的圖象與性質,并嘗試解決相關問題.
請將以下過程補充完整:
(1)判斷這個函數的自變量x的取值范圍是________________;
(2)補全表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)在平面直角坐標系![]() 中畫出函數
中畫出函數![]() 的圖象:
的圖象:
(4)填空:當![]() 時,相應的函數解析式為___(用不含絕對值符合的式子表示);
時,相應的函數解析式為___(用不含絕對值符合的式子表示);
(5)寫出直線![]() 與函數
與函數![]() 的圖象的交點坐標.
的圖象的交點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC 中,AB=AC,過其中一個頂點的直線可以把這個三角形分成另外兩個等腰三角形,則∠BAC( )
A. 36°,90°,![]() , 108°B. 36°,72°,
, 108°B. 36°,72°,![]() ,90°
,90°
C. 90°,72°,108°,![]() D. 36°,90°,108°,
D. 36°,90°,108°,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
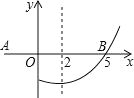
【題目】如圖是拋物線 y=ax![]() +bx+c 的一部分,其對稱軸為直線 x=2,若其與 x 軸的一個交點為(5,0),則由圖象可知,不等式 ax
+bx+c 的一部分,其對稱軸為直線 x=2,若其與 x 軸的一個交點為(5,0),則由圖象可知,不等式 ax![]() +bx+c<0 的解集是________.
+bx+c<0 的解集是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
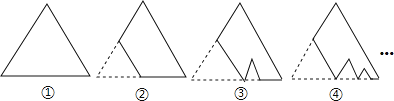
【題目】如圖,圖①是一塊邊長為1,周長記為P1的等邊三角形紙板,沿圖①的底邊剪去一塊邊長的![]() 的等邊三角形紙板后得到圖②,然后沿同一底邊依次剪去一塊更小的等邊三角形紙板(即其邊長為前一塊被剪掉等邊三角形紙板邊長的
的等邊三角形紙板后得到圖②,然后沿同一底邊依次剪去一塊更小的等邊三角形紙板(即其邊長為前一塊被剪掉等邊三角形紙板邊長的![]() )后,得圖③,④,…,記第n(n≥3)塊紙板的周長為Pn,則Pn-Pn-1=_________
)后,得圖③,④,…,記第n(n≥3)塊紙板的周長為Pn,則Pn-Pn-1=_________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人分別從A,B兩地同時出發,勻速相向而行.甲的速度大于乙的速度,甲到達B地后,乙繼續前行.設出發xh后,兩人相距ykm,圖中折線表示從兩人出發至乙到達A地的過程中y與x之間的函數關系.
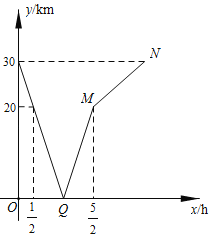
(1)根據圖中信息,求出點Q的坐標,并說明它的實際意義;
(2)求甲、乙兩人的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
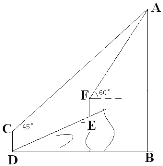
【題目】如圖,在一次數學課外實踐活動中,要求測量山坡前某建筑物的高度AB.小剛在D處用高1.5m的測角儀CD,測得該建筑物頂端A的仰角為45°,然后沿傾斜角為30°的山坡向上前進20m到達E,重新安裝好測角儀后又測得該建筑物頂端A的仰角為60°.求該建筑物的高度AB.(結果保留根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com